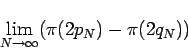Next: A LIMIT COMPARISON THEOREM
Up: On Rearrangements of Conditionally
Previous: THE MAIN RESULT
In this section we will use Theorem 1 to investigate the convergence of rearrangements of some prominent alternating series. In all cases we do the explicit proofs for 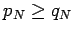 (at least eventually). We mention that the other situation can be handled in the same way. The most prominent -- and most intensively investigated -- conditionally convergent series is the alternating harmonic series, indeed several of the papers cited specialize on this topic [3,5]. As we will later see this series is not a very good model, since it is converging so rapidly, in fact it is almost absolutely convergent. Applying Theorem 1 to that series yields the following result.
(at least eventually). We mention that the other situation can be handled in the same way. The most prominent -- and most intensively investigated -- conditionally convergent series is the alternating harmonic series, indeed several of the papers cited specialize on this topic [3,5]. As we will later see this series is not a very good model, since it is converging so rapidly, in fact it is almost absolutely convergent. Applying Theorem 1 to that series yields the following result.
Corollary 2
For the alternating harmonic series the statement of Theorem 1 becomes:
Proof: In this case 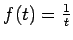 and
and 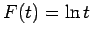 . Applying Theorem 1 gives
. Applying Theorem 1 gives

In particular, this Corollary implies that the limit of a rearrangement of the alternating harmonic series is finite, if and only if
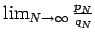 is finite.
Other authors do not use the ratio we use in this paper, but rather use the asymptotic density of positive terms in the rearrangement, which is defined as
is finite.
Other authors do not use the ratio we use in this paper, but rather use the asymptotic density of positive terms in the rearrangement, which is defined as
In this notation, the above corollary implies that a rearrangement of the alternating series converges to a finite limit if and only if 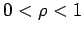 . The alternating harmonic series is a relatively rapidly converging alternating series and represents as such a limiting case for conditionally convergent series. Corollary 1 also allows us to compute explicit rearrangements converging to a given number. Since in this case it is known that
. The alternating harmonic series is a relatively rapidly converging alternating series and represents as such a limiting case for conditionally convergent series. Corollary 1 also allows us to compute explicit rearrangements converging to a given number. Since in this case it is known that 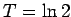 . For example, to construct a rearrangement which converges to
. For example, to construct a rearrangement which converges to 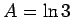 we must ensure that
we must ensure that
This can easily be achieved by taking always 9 positive terms followed by 4 negative terms.
In our next example we will investigate a class of slower converging 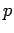 -series.
-series.
Corollary 3
Consider the alternating 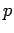 - series
with
- series
with 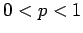 . Then a rearrangement of this series converges to a finite limit if and only if
i.e.
. Then a rearrangement of this series converges to a finite limit if and only if
i.e. 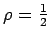 .
.
Proof: In this case 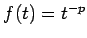 and hence
and hence
The theorem implies that
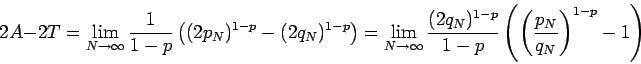 |
(7) |
Since
grows without bound as 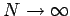 , the limit in (7) can only be finite if
, the limit in (7) can only be finite if
which proves our assertion. The statement in terms of the asymptotic density 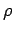 follows immediately.
follows immediately.

In the case of the alternating harmonic series, convergence of a rearrangement is assured if
is a finite positive number. In Corollary 3, this number must be one. This suggests that there are really at most three classes of conditionally convergent series, Namely series where a rearrangement converges to a finite limit if and only if
and
series for which rearrangements converge if and only if this limit is a finite positive number. Finally, there is the possibility of series for which a rearrangement also converges if the limit is either 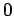 or if the sequence
or if the sequence
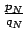 is unbounded. We will encounter aan example of such a series later in this section.
is unbounded. We will encounter aan example of such a series later in this section.
We will now extend these results to another prominent set of alternating series.
Corollary 4
Let 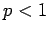 and consider the series
A rearrangement of this series converges to a finite limit if and only if
and consider the series
A rearrangement of this series converges to a finite limit if and only if
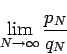 |
(8) |
is finite and positive.
Proof: Observe that
The previous Corollary implies that a rearrangement of
converges to a finite limit if and only if
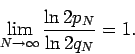 |
(9) |
Before continuing we remark that unlike in the previous corollary we can allow 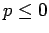 here, since the original alternating series also converges in this case and the argument of the proof of Corollary 3 still works.
here, since the original alternating series also converges in this case and the argument of the proof of Corollary 3 still works.
We are left to show the equivalence of (9) and (8). To do this suppose first that
for some positive real number 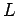 . Next choose
. Next choose 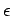 such that
such that 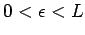 . Then there exists an
. Then there exists an 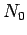 such that
such that
for all 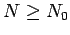 . Multiplication with
. Multiplication with 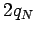 yields
yields
for all 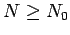 . The logarithm is a strictly monotonically increasing function. Thus previous inequality implies
. The logarithm is a strictly monotonically increasing function. Thus previous inequality implies
and
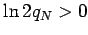 for sufficiently large
for sufficiently large 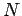 , thus we may divide the inequality by this quantity to get
, thus we may divide the inequality by this quantity to get
for all 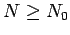 . We take the limit as
. We take the limit as 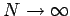 and get (9).
and get (9).
To show the opposite direction assume that
is unbounded. Then there exists an 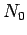 such that
such that
for all 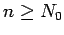 . Next observe that for every
. Next observe that for every 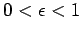 we have
we have
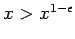 for all
for all 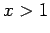 . This implies that
. This implies that
for all 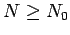 . Thus
. Thus
for all 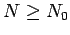 . Since this inequality holds for all
. Since this inequality holds for all 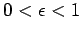 it follows that
it follows that
This implies the contrapositive of
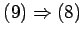 . If
. If
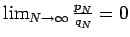 , we apply the same argument to
, we apply the same argument to
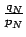 . This completes the proof of the Corollary.
. This completes the proof of the Corollary.

This last Corollary cannot be extended to the case 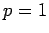 . In that case convergence of a rearrangement is equivalent to
the condition
. In that case convergence of a rearrangement is equivalent to
the condition
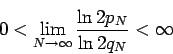 |
(10) |
by Corollary 2. However, (10) is much weaker than (8). To see this consider the case when
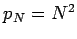 and
and 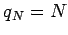 . Then
. Then
and
which is unbounded. These sequences do not satisfy 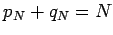 , but the sequences
, but the sequences
![$q_N=[\sqrt{N}]$](img105.png) and
and 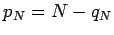 do and allow us to
construct a rearrangement of the series
do and allow us to
construct a rearrangement of the series
which converges to a finite number with unbounded
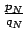 .
.
We finish this section by studying the series
A straight forward application of Theorem 1 gives that a rearrangement with a sequence of positive terms 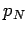 and negative terms
and negative terms 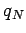 converges to a finite number, if and only if
converges to a finite number, if and only if
exists and is finite. Here 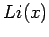 denotes the logarithmic integral function defined as
denotes the logarithmic integral function defined as
Using l'Hospital's rule we get
and therefore the rearrangement converges if and only if
exists and is finite. Factoring this expression as before we get
which can only be finite if
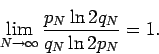 |
(11) |
From the proof of the last Corollary we have that if
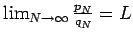 for some finite positive number
for some finite positive number 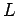 , then
, then
It follows that in this case (11) holds if and only if 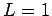 . However,
(11) could hold if
. However,
(11) could hold if
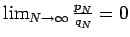 or if it diverges.
To investigate this case let
or if it diverges.
To investigate this case let
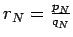 , and assume that
, and assume that 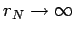 then
then
Clearly, this expression diverges if 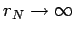 . On the other hand if
. On the other hand if 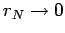 we investigate the reciprocal of this expression in the same way. Therefore (11) can never be satisfied. We have thus shown
we investigate the reciprocal of this expression in the same way. Therefore (11) can never be satisfied. We have thus shown
Corollary 5
A rearrangement of
converges if and only if
This last result has a slightly different interpretation in light of the prime number theorem. Let 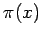 denote the number of primes that are less than or equal to
denote the number of primes that are less than or equal to 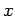 , then the prime-number theorem [1, p. 74] implies that a rearrangement of this series converges if and only if
, then the prime-number theorem [1, p. 74] implies that a rearrangement of this series converges if and only if
is finite. Or in other words if 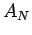 is the number of primes in the interval
is the number of primes in the interval ![$[2q_N,2p_n]$](img128.png) , then the rearrangement converges if and only if
, then the rearrangement converges if and only if
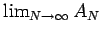 is finite.
is finite.



Next: A LIMIT COMPARISON THEOREM
Up: On Rearrangements of Conditionally
Previous: THE MAIN RESULT
Werner Horn
2006-11-20
![]() (at least eventually). We mention that the other situation can be handled in the same way. The most prominent -- and most intensively investigated -- conditionally convergent series is the alternating harmonic series, indeed several of the papers cited specialize on this topic [3,5]. As we will later see this series is not a very good model, since it is converging so rapidly, in fact it is almost absolutely convergent. Applying Theorem 1 to that series yields the following result.
(at least eventually). We mention that the other situation can be handled in the same way. The most prominent -- and most intensively investigated -- conditionally convergent series is the alternating harmonic series, indeed several of the papers cited specialize on this topic [3,5]. As we will later see this series is not a very good model, since it is converging so rapidly, in fact it is almost absolutely convergent. Applying Theorem 1 to that series yields the following result.
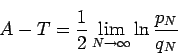
![]() and
and ![]() . Applying Theorem 1 gives
. Applying Theorem 1 gives
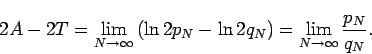
![]()
![]() is finite.
Other authors do not use the ratio we use in this paper, but rather use the asymptotic density of positive terms in the rearrangement, which is defined as
is finite.
Other authors do not use the ratio we use in this paper, but rather use the asymptotic density of positive terms in the rearrangement, which is defined as
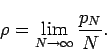
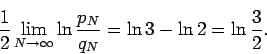
![]() -series.
-series.
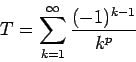
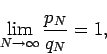
![]() and hence
and hence
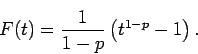
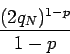
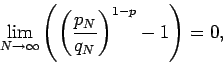
![]()
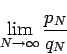
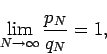
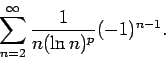
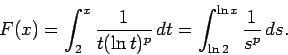
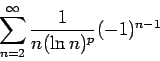
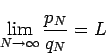
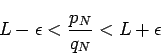
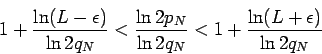
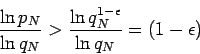
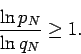
![]()
![]() . In that case convergence of a rearrangement is equivalent to
the condition
. In that case convergence of a rearrangement is equivalent to
the condition
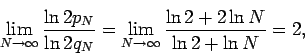
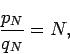
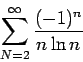
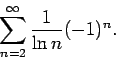
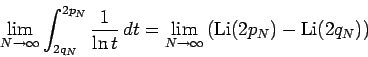
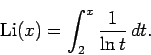
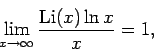
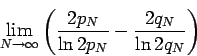
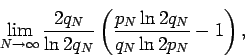
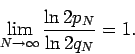
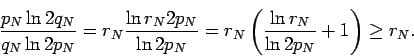
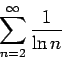
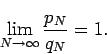
![]() denote the number of primes that are less than or equal to
denote the number of primes that are less than or equal to ![]() , then the prime-number theorem [1, p. 74] implies that a rearrangement of this series converges if and only if
, then the prime-number theorem [1, p. 74] implies that a rearrangement of this series converges if and only if