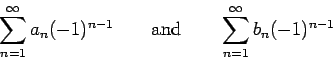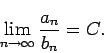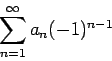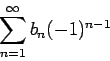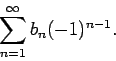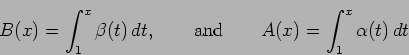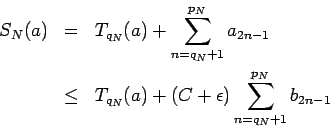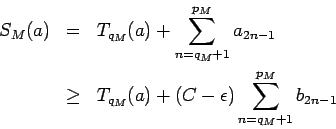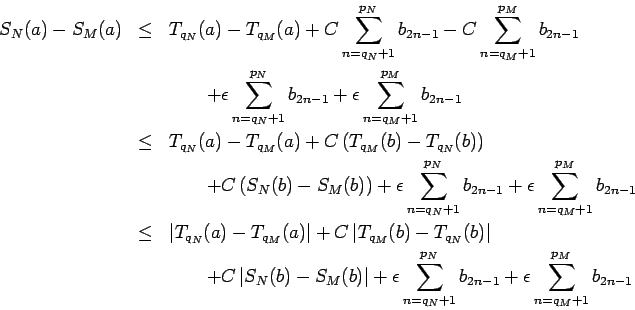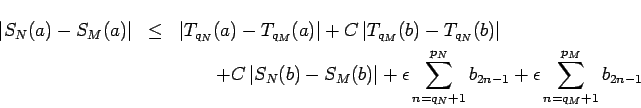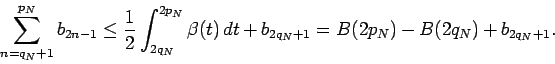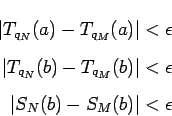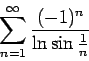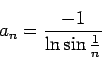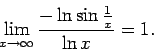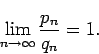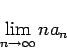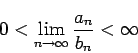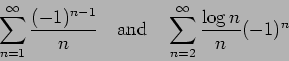Next: Bibliography
Up: On Rearrangements of Conditionally
Previous: EXAMPLES AND CONSEQUENCES
In the previous section we considered the convergence behavior of some special series. This section is devoted to a more general convergence result. Similar to the rich theory of the convergence of positive series, we will prove a comparison theorem. This will allow us to study the convergence of rearrangements of series with more complicated terms.
Theorem 2
Let
be two conditionally convergent series, which satisfy the assumptions spelled out in the introduction of this paper.
Assume that there is a positive constant 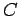 such that.
Then any rearrangement of
will converge if and only if the corresponding rearrangement of
converges.
such that.
Then any rearrangement of
will converge if and only if the corresponding rearrangement of
converges.
Proof: To facilitate the proof of this theorem we need to introduce some notation. Consider a given rearrangement of the alternating series
with associated sequence s 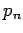 and
and 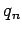 of positive and negative terms.
Without loss of generality we assume that
of positive and negative terms.
Without loss of generality we assume that 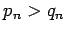 for sufficiently large
for sufficiently large 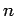 .
Let
.
Let
denote the 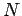 -th partial sum of this rearrangement, and
-th partial sum of this rearrangement, and
denote the 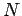 -th partial sum of the same rearrangement of
-th partial sum of the same rearrangement of
Moreover, let 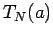 and
and 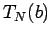 denote the partial sums of the corresponding alternating series. Furthermore, let
denote the partial sums of the corresponding alternating series. Furthermore, let
be two continuous functions with anti derivatives 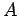 and
and 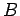 such that
such that
Finally, let
Let 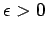 then there exists an
then there exists an 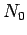 such that
such that
for all
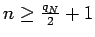 .
Let
.
Let 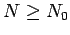 , then
, then
Analogously, we get
for 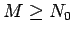 . Subtracting the second inequality from the first we get
. Subtracting the second inequality from the first we get
In this step we used the decomposition of 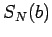 into
into  and a positive remainder term, and the fact that
and a positive remainder term, and the fact that 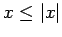 . On the right hand side of the last inequality we may interchange
. On the right hand side of the last inequality we may interchange 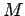 and
and 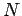 without changing the value of the right hand side. This implies that the same inequality applies to
without changing the value of the right hand side. This implies that the same inequality applies to
and therefore
Next, from the proof of Theorem 1 we have that
Now assume that 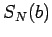 converges, then by Theorem 1
converges, then by Theorem 1
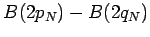 converges to
a finite number and hence there exists a
converges to
a finite number and hence there exists a 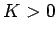 such that
such that
for all 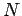 . Next, since
. Next, since 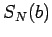 ,
, 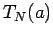 , and
, and 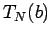 all converge, they are Cauchy sequences and there exists a
all converge, they are Cauchy sequences and there exists a 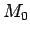 such that
such that
Hence, for
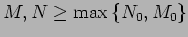
and therefore it is a Cauchy sequence and it converges. The opposite direction is proved completely analogously.

We illuminate the use of Theorem 2 by an example. Consider the series
The reader can easily verify that
satisfies the conditions of both theorems. Now using l'Hospital's rule we get
Therefore, by Corollary 6, any rearrangement of this series converges if and only if
Remarks:
- To best of our knowledge, Theorem 2 is, at least in the form given, a new result, albeit not very useful. A. Pringsheim [7] does a comparison of conditionally convergent series with the alternating harmonic series, by comparing whether
is finite or not. This result follows from Theorem 2 by using the alternating harmonic series as one of the two series used in Theorem 2.
- The condition that
is only a sufficient condition for rearrangements of the two series two converge together. As we have seen in Corollaries 2 and 3 rearrangements of,
converge together, but the condition of Theorem 2 is obviously not satisfied.
- The entire paper only applies to series with eventually decreasing terms. There are, however series which do not satisfy this property and which are still conditionally convergent and subject to Riemann's Theorem.



Next: Bibliography
Up: On Rearrangements of Conditionally
Previous: EXAMPLES AND CONSEQUENCES
Werner Horn
2006-11-20