


Next: EXAMPLES AND CONSEQUENCES
Up: On Rearrangements of Conditionally
Previous: INTRODUCTION
To state and prove the main result we will first introduce some notation, namely let
be a non-negative sequence, that converges to zero and is eventually decreasing.Moreover, let 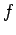 be a continuous, non-negative, and eventually decreasing function on
be a continuous, non-negative, and eventually decreasing function on 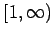 such that
such that
for all positive integers 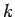 . Such a function will always exist, since one can just take the piecewise linear function connecting the points
. Such a function will always exist, since one can just take the piecewise linear function connecting the points 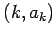 . Define
. Define
The alternating series
converges by the alternating series test. If in addition 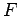 is bounded the series converges absolutely.
is bounded the series converges absolutely.
To continue let
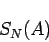 |
(2) |
be the 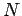 -th partial sum of a rearrangement of the series that converges to a real number
-th partial sum of a rearrangement of the series that converges to a real number 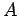 , and let
, and let
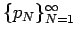 and
and
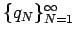 be the related sequences of positive and negative terms mentioned above. It is easily checked that
be the related sequences of positive and negative terms mentioned above. It is easily checked that
and
We can now state the main result of this note:
Theorem 1
With the notations introduced above we have:
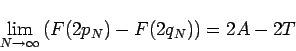 |
(3) |
Proof: Without loss of generality, we will assume that 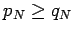 for all sufficiently large values of
for all sufficiently large values of 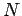 . The other case can be shown in the completely analogous way. We have
. The other case can be shown in the completely analogous way. We have
where 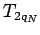 is the
is the 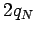 -th partial sum for the original alternating series.
From Figure 1 below we see that
-th partial sum for the original alternating series.
From Figure 1 below we see that
and therefore
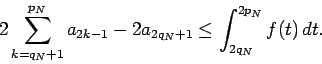 |
(4) |
Figure 2 shows that
and therefore
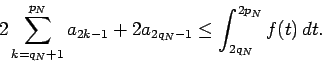 |
(5) |
Figure 1:
Upper estimate of the sum by the integral
|
|
Figure 2:
Lower estimate of the sum by the integral
|
|
Combining (4) and (5), we obtain
which immediately implies
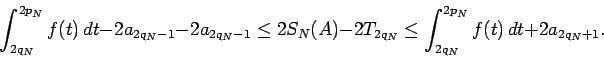 |
(6) |
Finally, we observe that
Therefore the desired result follows from taking the limit as 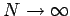 in all terms of (6).
in all terms of (6).

Corollary 1
If
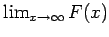 exists and is finite, the series is absolutely convergent, and
Therefore, any rearrangement of an absolutely convergent series converges to the same limit.
exists and is finite, the series is absolutely convergent, and
Therefore, any rearrangement of an absolutely convergent series converges to the same limit.
Proof: In this case we have
and the result follows immediately.




Next: EXAMPLES AND CONSEQUENCES
Up: On Rearrangements of Conditionally
Previous: INTRODUCTION
Werner Horn
2006-11-20
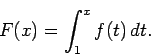
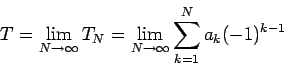
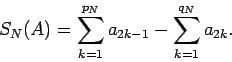
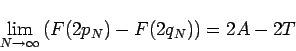
![]() for all sufficiently large values of
for all sufficiently large values of ![]() . The other case can be shown in the completely analogous way. We have
. The other case can be shown in the completely analogous way. We have
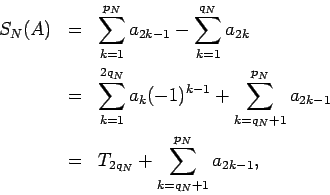
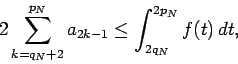
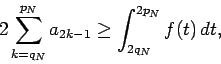
![\includegraphics[scale=0.2]{lower.eps}](img35.png)
![\includegraphics[scale=0.2]{upper.eps}](img36.png)
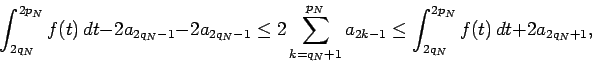
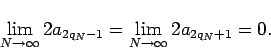
![]()
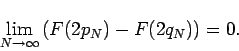
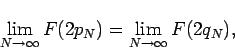
![]()