


Next: THE MAIN RESULT
Up: On Rearrangements of Conditionally
Previous: On Rearrangements of Conditionally
In most calculus courses students learn that the terms of a conditionally convergent series
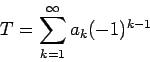 |
(1) |
may be rearranged to converge to any given real number. This result is somewhat mysterious as it seems to contradict our experience. After all the commutativity of addition of real numbers is one of the truth', which we hold as self-evident. Why should this principle break down, when the sum contains an infinite number of terms. Surprisingly, the proof of this result is relatively easy and we will start with a rough sketch of it before shedding some different light on this result.
If the sequence
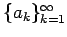 is a decreasing (or at least eventually decreasing) positive sequence that converges to
is a decreasing (or at least eventually decreasing) positive sequence that converges to 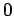 , and
, and 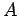 is a positive real number, one obtains a rearrangement that converges to
is a positive real number, one obtains a rearrangement that converges to 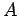 by first adding odd (positive) terms in the series until
by first adding odd (positive) terms in the series until
and
In the next step one subtracts one or more of the negative terms until the sum is less than 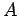 . One continues this process by adding positive terms until the sum exceeds
. One continues this process by adding positive terms until the sum exceeds 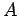 and subtracting negative terms until it is less than
and subtracting negative terms until it is less than 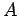 again.
In this manner
again.
In this manner 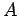 becomes sandwiched between the partial sums ending with a negative term and the ones ending with a positive term. And since
becomes sandwiched between the partial sums ending with a negative term and the ones ending with a positive term. And since 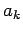 is decreasing to zero, the difference of these partial sums will also go to zero. We refer the reader to [6, pp. 318-319] or [4, p. 518] for a complete proof of this result.
is decreasing to zero, the difference of these partial sums will also go to zero. We refer the reader to [6, pp. 318-319] or [4, p. 518] for a complete proof of this result.
In this paper we will investigate this result from a slightly different angle. For a given rearrangement the 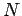 -th partial sum
-th partial sum
contains a unique number 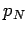 of positive terms and
of positive terms and 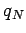 of negative terms. In this way the rearrangement can be identified with two sequences of integers
of negative terms. In this way the rearrangement can be identified with two sequences of integers
We will first prove a result that connects these sequences in a simple formula to the limit of the rearranged series.
This will allow us to compute limits of the series in an efficient way and will lead us to criteria for the convergence of rearrangements. These results are not original, and similar results on the relation between the limits of the series and these two sequences (or related sequences) have appeared in the literature before. A rather complete treatment of these and related problems was given by A. Pringsheim as early 1883 [7]. However, this paper is not easily accessible to most students, as it was written in German and in a rather archaic style. More recent works on this and related subjects are [2,3,8]. Despite the richness of the literature, we felt that the subject deserves further investigation.
The proofs of the theorems in this paper are completely elementary and accessible to anyone with a strong background in calculus. In the next section we will state and prove the main result on the relationship between the limits of the series and the sequences
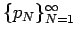 and
and
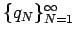 .
The third section of the paper will cover some consequences and simple examples. In the final section we will use the earlier results to prove a limit comparison theorem for rearrangements of series. We will limit ourselves to series with decreasing or eventually decreasing terms.
.
The third section of the paper will cover some consequences and simple examples. In the final section we will use the earlier results to prove a limit comparison theorem for rearrangements of series. We will limit ourselves to series with decreasing or eventually decreasing terms.



Next: THE MAIN RESULT
Up: On Rearrangements of Conditionally
Previous: On Rearrangements of Conditionally
Werner Horn
2006-11-20
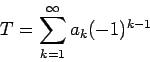
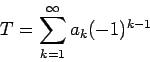
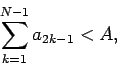
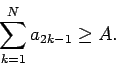
![]() -th partial sum
-th partial sum