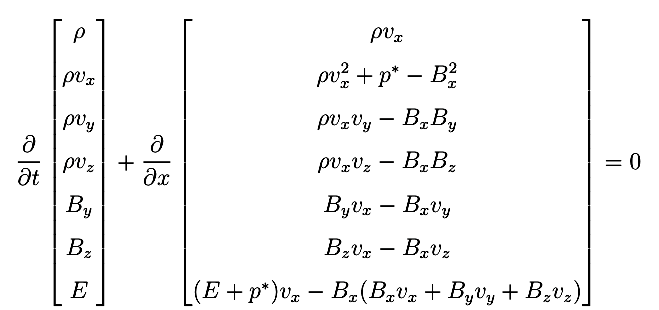Asst. Professor
Department of Mathematics
California State University, Northridge
|
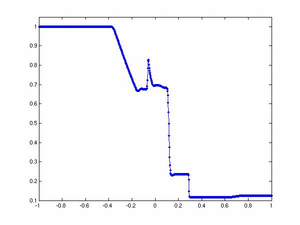
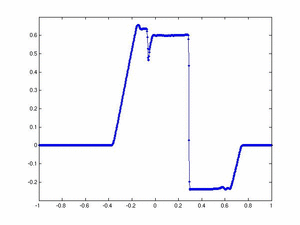
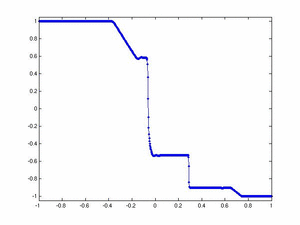
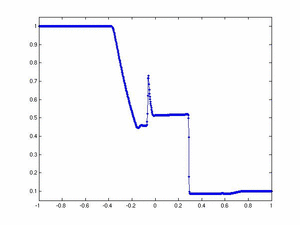
One Dimensional Ideal MHD Equations In this example we use a one-dimensional second order fully-discrete central scheme to evolve the solution of the equations of Ideal Magnetohydrodynamics
where
stands for the total pressure, and the the pressure, p, is related to the conserved quantities through the equation of state
with
and Dirichlet boundary conditions (i.e., the conserved quantities take on the values specified by the initial conditions at either boundary). Solution computed with 400 cells and cfl number 0.475. The images below display, from top to bottom and left to right, the profiles of density, x-velocity, y-velocity, y-magnetic field, and pressure at Click on the images to see an animation
|