Math
Math 094 Mod. III - Chapter 1  

Fractions (Module III, page 3) 

1.1 Definition of a fraction :
The first sentence on page 3 of Module III says that a fraction is of the form  where a is an integer and b is a natural number ... Why a natural number in the denominator ? This is important because we never want 0 in the denominator of a fraction ( remember the natural numbers are 1, 2, 3 ...Thus 0 is not a natural number ). Important definitions in chapter 1 of Module III are Numerator , Denominator , Proper and Improper and Equivalent fractions . Where are proper fractions found on the number line ? (see pg. 3) Where are improper fractions found on the real number line ?

1.2 More Fractions

I will expect to see all fractions in this course reduced to LOWEST TERMS . A fraction is reduced to lowest terms when the GCF of the numerator and denominator is 1 . For example ,  is a fraction that is not reduced to lowest terms . This is

because the GCF of 51 and 72 is not 1 . What is the GCF of 51 and 72 ? ( GCF was explained in Module II chapter 4 ) . Often it is easy to see that a fraction is not reduced such as  which we know reduces to  .

But what about ? In this case I recommend you break the numerator and denominator into their prime factorizations :

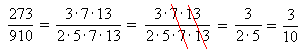
You will not be allowed to use a calculator on the tests . I strongly recommend that you do not use it with your homework either . Doing multiplication in your head and on paper is often tedious but the more you exercise these skills the easier it gets. Make sure you know your basic times tables.

WARNING : A common mistake I see in reducing fractions is as follows ...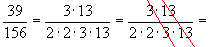

everything on top canceled so it is thought that the numerator is 0 .

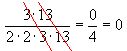This is NOT correct !!

When a number in the numerator cancels with a number in the denominator the result is 1 !!

So the correct answer is

1.3 Adding and Subtracting Fractions

Adding and subtracting fractions requires that the fractions have common denominators. Page 7 of module III shows how to use the LCM of the two denominators as the common denominator. Remember to reduce after adding , subtracting , multiplying or dividing fractions .

Example: (see Mod. III, page 7 and 8)

1.4. Multiplying and Dividing Fractions

Multiplying fractions:

Example: (see Mod. III, page 9 and 10)