The following are originally developped by Marty Tippens and used per his permission.
Math 094 - Mod. II - Chapter 4
reatest Common Factor ( see Module II, page 29)The procedure for finding the GCF is as follows:
1. Find the prime factorization of each number (use prime factor tree method in Ch. 3 )
2. Identify COMMON primes.
3. Pull the common primes with the least power.
4. The product of step 3 is the GCF .
Go over the examples in the module . You will be finding GCF's and LCM's from now through the end of the semester .
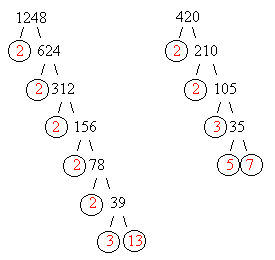
Example: The following is an example that uses the tree method .
...........................................
From the tree we see that the prime factorization of
1248 =![]() and
and
420 = ![]() .
.
GCF = ![]()
(The primes common to both numbers are 2 and 3 . But 2 is not the GCF! We need to take the least exponent attached to a 2 , in this case that means 2 . Thus ![]() is the GCF of 1248 and 420.)
is the GCF of 1248 and 420.)
Note: With two numbers as large as 420 and 1248 is may seem strange that the biggest number that divides evenly into both numbers is 4.But what about 1248 and 1249 ? The biggest number that divides evenly into both of these numbers is 1 ! Why ?
east Common Multiple (Module II, page 31)
The procedure for finding the LCM is as follows:
1. Find the prime factorization of each number (use prime factor tree method )
2. List ALL primes used in either of the numbers .
3. Attach the highest exponents belonging to each given prime .
4. The product of these primes with highest exponents is the LCM.
.
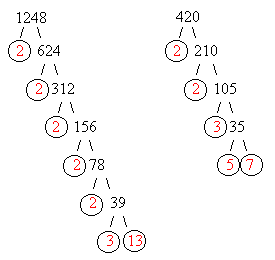
Example: To find the LCM of 1248 and 420 find the prime factors as follows :
 ...
...
Thus the prime factorization of
1248 =![]() and
and
420 = ![]()
LCM = ![]()
(Following the procedure to step 2 we take ALL primes in each factorization and list them : 2 , 3 , 5 , 7 , 13 . These are the different numbers that were circled above. Now we take the highest exponent belonging to each prime . The highest exponent belong to 2 is 5 . The highest exponent belonging to 3, 5, 7, and 13 is 1 ( a number with no exponent actually has the "implied" exponent 1). Hence the LCM of 1248 and 420 is ![]() .
.
Practice Problem:
#1 Find the GCF of {72, 630, 378}
#2 Find the LCM of {72, 630, 378}
#1 Find the prime factorization of {72, 630, 378}first:
72 = ![]()
630 = ![]()
378 = ![]()
Common prime are 2 and 3. The least exponent attached to 2 is 1 and the least exponent attached to 3 is 2. Therefore,
GCF = ![]() =
= ![]() = 18.
= 18.
#2 List ALL prime from above: 2, 3, 5, 7, then take the highest exponent attached to each prime, which is 3, 2, 1 and 1 respectively. Therefore,
LCM = ![]() . You may leave your answer in exponential form.
. You may leave your answer in exponential form.