A nonlinear pendulum

Contents

The differential equation:
The corresponding system of the first order differential equations:
Input initial conditions:
Define the interval on which solution is computed:
Solve the system using ode45 procedure:
Extract the positions and velocities:
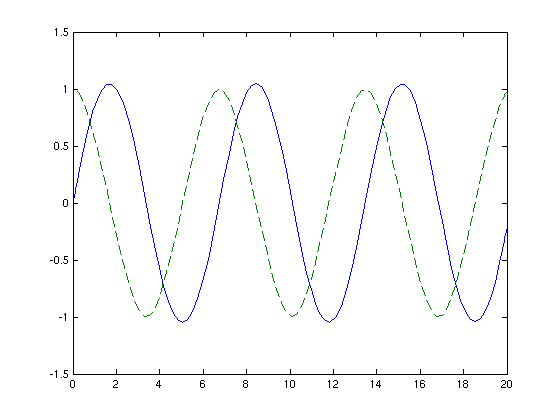
Plots of the positions and velocities as functions of time:
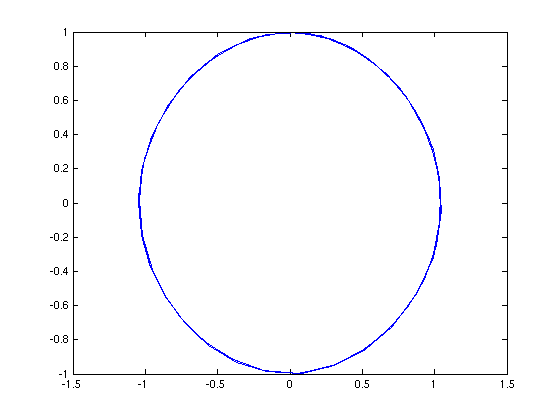
Plot of the phase portrait (velocity as the function of position):

The differential equation:

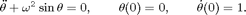
$\ddot{\theta}+\omega^2\sin\theta=0,\qquad \theta(0)=0,\qquad \dot{\theta}(0)=1.$

The corresponding system of the first order differential equations:

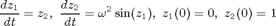
$\frac{dz_1}{dt}=z_2,\,\, \frac{dz_2}{dt}=-\omega^2\sin(z_1),\,\, z_1(0)=0,\,\, z_2(0)=1$

Input initial conditions:

z0=[0,1];

Define the interval on which solution is computed:

tspan =[0,20];

Solve the system using `ode45` procedure:

[t,z] = ode45('ode3',tspan,z0);

Extract the positions and velocities:

x=z(:,1); v=z(:,2);

Plots of the positions and velocities as functions of time:

Note: The dashed curve indicates velocities

plot(t,x,t,v,'--')

Plot of the phase portrait (velocity as the function of position):

figure(2)
plot(x,v)