

The graph of a quadratic equation in two variables (y = ax2 + bx + c ) is called a parabola. The following graphs are two typical parabolas their x-intercepts are marked by red dots, their y-intercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot:


We say that the first parabola opens upwards (is a U shape) and the second parabola opens downwards (is an upside down U shape). In order to graph a parabola we need to find its intercepts, vertex, and which way it opens.
Given y = ax2 + bx + c , we have to go through the following steps to find the points and shape of any parabola:
If a > 0 (positive) then the parabola opens upward.
If a < 0 (negative) then the parabola opens downward.
Notice that the x-intercepts of any graph are points on the x-axis and therefore have y-coordinate 0. We can find these points by plugging 0 in for y and solving the resulting quadratic equation (0 = ax2 + bx + c). If the equation factors we can find the points easily, but we may have to use the quadratic formula in some cases. If the solutions are imaginary, that means that the parabola has no x-intercepts (is strictly above or below the x-axis and never crosses it). If the solutions are real, but irrational (radicals) then we need to approximate their values and plot them.
The y-intercept of any graph is a point on the y-axis and therefore has x-coordinate 0. We can use this fact to find the y-intercepts by simply plugging 0 for x in the original equation and simplifying. Notice that if we plug in 0 for x we get: y = a(0)2 + b(0) + c or y = c. So the y-intercept of any parabola is always at (0,c).
To find the x-coordinate for the vertex we use the following formula:
![]()
To find the y-coordinate for the vertex we plug in h in the original equation:
k = a(h)2 + b(h) + c
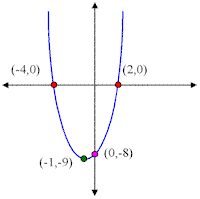
Example 1) Graph y = x2 + 2x - 8
In this problem: a = 1, b = 2 , and c = -8.
Since "a" is positive we'll have a parabola that opens upward (is U shaped).
To find the x-intercepts we plug in 0 for y:
0 = x2 + 2x - 8 (which factors)
0 = (x + 4)(x - 2)
x = -4 or x = 2
So this parabola has two x-intercepts: (-4,0) and (2,0).
To find the y-intercept we plug in 0 for x:
y = (0)2 + 2(0) - 8 = -8
So the y-intercept of the parabola is (0,-8).
To find the vertex we use: ![]()
![]() and to find k, we plug in -1 in for x:
and to find k, we plug in -1 in for x:
k = (-1)2 + 2(-1) - 8
k = 1 - 2 - 8 = -9
The vertex of this parabola is at (-1, -9)
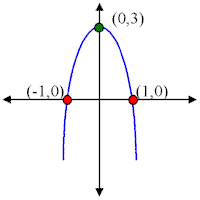
Example 2) Graph y = -3x2 + 3
In this problem a = -3, b = 0 and c = 3.
Since "a" is negative this parabola is going to open downward (upside down U shape).
To find the x-intercepts we plug in 0 for y:
0 = -3x2 + 3 (this equation factors)
0 = -3(x2 - 1)
0 = -3(x - 1)(x + 1) and since -3 can not equal zero:
x = 1 or x = -1
The x-intercepts are: (1,0) and (-1,0)
The y-intercept is found by plugging 0 for x:
y = -3(0)2 + 3 = 3
So, the y-intercept is at (0,3).
And to find the vertex:
![]()
k = -3(0)2 + 3 = 3
So the vertex is at (0,3).
Notice that in this problem the vertex and the y-intercept are the same point.
Example 3) Graph y = x2 + 4x + 7
a = 1, b = 4, and c = 7
Since a 0 the parabola opens up (is U shaped).
To find the x -intercept we plug in 0 for y:
0 = x2 + 4x + 7 (this expression does not factor so we have to use the quadratic formula)

Since the roots are imaginary the parabola has no x-intercepts.
We find the y-intercepts by plugging in 0 for x:
y = 02 + 4(0) + 7 = 7
The y-intercept is (0,7).
The vertex:

So the vertex is at (-2, 3).
