When finding the volume of a solid of revolution of a graph like that of

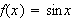 on
on

![$[0,\pi ]$](f3b2__2.png) you can use the computer to graph the area being revolved about the
you can use the computer to graph the area being revolved about the

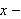 axis
as well as the solid for which you wish to compute the volume.
axis
as well as the solid for which you wish to compute the volume.
-
Graph

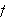 and adjust the viewing rectangle to show the graph only on the given interval.
and adjust the viewing rectangle to show the graph only on the given interval.
-
Graph the solid of revolution obtained when

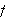 restricted to domain
restricted to domain

![$[0,\pi ]$](f3b2__6.png) is revolved about the
is revolved about the

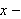 axis.
(Hint: To plot a solid of revolution generated by rotating
axis.
(Hint: To plot a solid of revolution generated by rotating

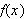 about the x-axis we create the vector
about the x-axis we create the vector

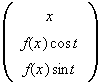 and plot it using Compute: Plot3D+Rectangular.)
and plot it using Compute: Plot3D+Rectangular.)
For the following, adjust the viewing rectangles to show only the graphs on the restricted domains.
-
Graph

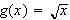 on
on

![$[0,16]$](f3b2__11.png) .
.
-
Graph the solid of revolution obtained when

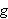 restricted to domain
restricted to domain

![$[0,16]$](f3b2__13.png) is revolved about the
is revolved about the

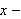 axis.
axis.
For the following, adjust the viewing rectangles to show only the graphs on the restricted domains.
-
Graph

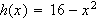 on
on

![$[-4,4]$](f3b2__16.png) .
.
-
Graph the solid of revolution obtained when

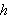 restricted to domain
restricted to domain

![$[-4,4]$](f3b2__18.png) is revolved about the
is revolved about the

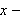 axis.
axis.
You can think of solids of revolution as using a certain amount of surface area to enclose a certain amount of volume.
This leads to the question of what function

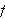 over what interval leads to a solid of revolution enclosing as much volume
over what interval leads to a solid of revolution enclosing as much volume

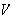 as possible while using as little surface area
as possible while using as little surface area

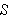 as possible. We can make this precise by studying the ratio
as possible. We can make this precise by studying the ratio

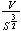 .
It turns out that this fraction never goes above a certain limit regardless of
the function
.
It turns out that this fraction never goes above a certain limit regardless of
the function

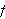 that is used. We can use the computer to experiment with various possibilities
for
that is used. We can use the computer to experiment with various possibilities
for

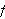 to see how much volume a solid of revolution can enclose using a certain
amount of area.
to see how much volume a solid of revolution can enclose using a certain
amount of area.
-
The assumption is made that

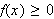 on
on

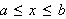 ,
and that the graph of
,
and that the graph of

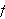 over this interval is being revolved about the
over this interval is being revolved about the

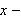 axis
to form a solid of revolution.
axis
to form a solid of revolution.
Since the disk method applies here, the volume is:

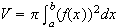 .
Evaluate the volumes of the solids in problems 1, 2, and 3 and record the
results in the table below.
.
Evaluate the volumes of the solids in problems 1, 2, and 3 and record the
results in the table below.


-
To find the total surface area for a given solid you must compute the "side" surface area given by

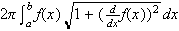 .
Then add the areas of the disks, if any, that form the "ends" of the solids.
The areas of these disks are
.
Then add the areas of the disks, if any, that form the "ends" of the solids.
The areas of these disks are

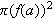 and
and

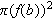 .
(Do you see why?) Thus, total surface area, which we
denote here by
.
(Do you see why?) Thus, total surface area, which we
denote here by

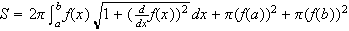 .
Find the total surface areas for problems 1, 2, and 3 and record the results
in the table above.
.
Find the total surface areas for problems 1, 2, and 3 and record the results
in the table above.
-
Compute

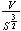 for problems 1, 2, and 3 and record the results in the table above.
for problems 1, 2, and 3 and record the results in the table above.
-
Experiment with functions of your own that you think will maximize

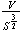 and
repeat parts (a) to (c) for those functions.
and
repeat parts (a) to (c) for those functions.
-
Make a conjecture about the maximum possible value of

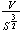 and what shape of curve gives this maximum.
and what shape of curve gives this maximum.