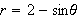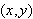 on the rectangular coordinate system. The corresponding equations for these
graphs have been in either rectangular or parametric form. Here we work with
the coordinate system called the polar coordinate
system.
on the rectangular coordinate system. The corresponding equations for these
graphs have been in either rectangular or parametric form. Here we work with
the coordinate system called the polar coordinate
system.
So far, we have been
representing graphs as collections of points

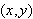 on the rectangular coordinate system. The corresponding equations for these
graphs have been in either rectangular or parametric form. Here we work with
the coordinate system called the polar coordinate
system.
on the rectangular coordinate system. The corresponding equations for these
graphs have been in either rectangular or parametric form. Here we work with
the coordinate system called the polar coordinate
system.
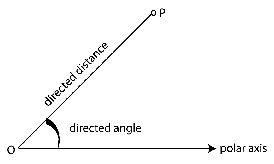
To form the polar coordinate system in the plane, we fix a point

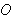 ,
called the origin, and construct from
,
called the origin, and construct from

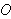 an initial ray called the polar axis. Then each point
an initial ray called the polar axis. Then each point

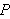 in the plane can be assigned polar coordinates
in the plane can be assigned polar coordinates

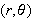 as follows.
as follows.

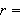 directed distance from
directed distance from

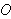 to
to

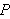

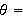 directed angle, counterclockwise from polar axis to
segment
directed angle, counterclockwise from polar axis to
segment

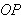
With rectangular coordinates,
each point

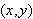 has a unique representation. This is not true with polar coordinates. For
instance, the coordinates
has a unique representation. This is not true with polar coordinates. For
instance, the coordinates

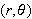 and
and

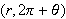 represent the same point. Also, because
represent the same point. Also, because

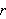 is a directed distance, the coordinates
is a directed distance, the coordinates

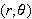 and
and

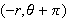 represent the same point.
represent the same point.
To establish the relationship between polar and rectangular coordinates, let
the polar axis coincide with the positive

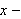 axis
and the pole with the origin. Because
axis
and the pole with the origin. Because

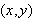 lies on a circle of radius
lies on a circle of radius

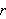 ,
it follows that
,
it follows that

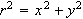 .
Moreover, for
.
Moreover, for

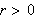 ,
the definition of the trigonometric functions implies that
,
the definition of the trigonometric functions implies that

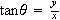 ,
,

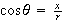 ,
and
,
and

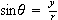 .
That is, the polar coordinates
.
That is, the polar coordinates

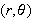 of a point are related to the rectangular coordinates
of a point are related to the rectangular coordinates

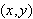 of the point as follows.
of the point as follows.

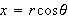 ,
,

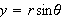 ,
,

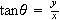 ,
and
,
and

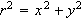 .
.
For the point

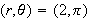 ,
,

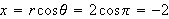 and
and

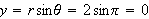 .
Thus the rectangular coordinates are
.
Thus the rectangular coordinates are

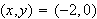 .
.
For the point

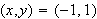 ,
,

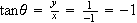 .
Thus,
.
Thus,

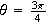 (since the original point is in the second quadrant).
(since the original point is in the second quadrant).

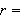

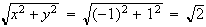 .
Thus, one set of polar coordinates is:
.
Thus, one set of polar coordinates is:

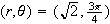 (recall that polar coordinates are not unique).
(recall that polar coordinates are not unique).
1. Convert the following rectangular coordinates to polar coordinates.
a.

 b.
b.

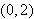
2. Convert the following polar coordinates to rectangular coordinates.
a.

 b.
b.

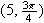
The following will be useful
for the next problem: If

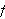 is
a differentiable function of
is
a differentiable function of

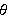 ,
then the slope of the tangent line to the graph of
,
then the slope of the tangent line to the graph of

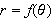 at
the point
at
the point

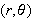 is
is

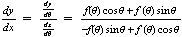 provided
that
provided
that

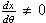 at
at

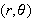 .
.
3. Graph the following polar equation and find all points of
horizontal tangency (that is, find the values of

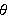 such that
such that

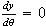 and
and

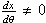 ).
).

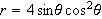
4. Graph the following polar equation. Find an interval for

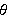 over which the graph is traced only once.
over which the graph is traced only once.

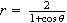
5. Graph the following polar equation so that you get the
curve depicted below. The curve is given by

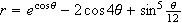 .
Over what interval must
.
Over what interval must

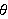 vary to produce the curve?
vary to produce the curve?
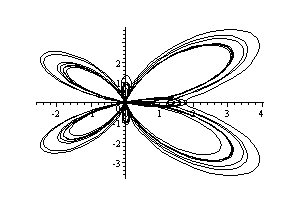
6. Heart to Bell Graph the polar
equation

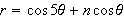 for
for

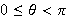 for the integers
for the integers

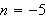 to
to

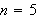 .
What values of
.
What values of

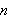 produce the "heart" portion of the curve? What values of
produce the "heart" portion of the curve? What values of

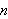 produce the "bell"?
produce the "bell"?
The following will be useful
for the next problem: If

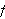 is
continuous and nonnegative on the interval
is
continuous and nonnegative on the interval

![$[\alpha ,\beta ]$](3b10__69.png) ,
then the area of the region bounded by the graph of
,
then the area of the region bounded by the graph of

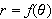 between
the radial lines
between
the radial lines

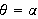 and
and

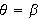 is
given by
is
given by

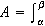

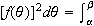

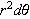 .
.
7. Graph the following polar equation and find the area of the indicated region.
a. Inner loop of

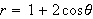 .
.
b. Between the loops of

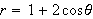
c. Inside

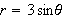 and outside
and outside