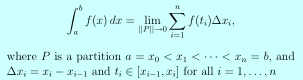
The definite integral can be defined as a limit of Riemann sums.
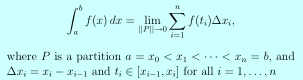
In the script below, enter the function f(x) and the endpoints of the interval [a,b] over which you want to work. When entering f(x), you can use +, -, *, /, ^, ( ), abs(), sin(), cos(), tan(), exp(), log(), log10(), asin(), acos(), atan(), pi, e. Take care to remember the * in all multiplications and to avoid discontinuities. Also, note that here, log() stands for the natural logarithm, while log10() stands for the common logarithm. When entering a and b, you can use integers or decimals. Pressing the "Plot" button will draw the graph of f(x). Then enter the number n of subintervals that [a,b] will be partitioned into, choose whether the partition will regular (all subintervals of the same length) or irregular (lengths chosen by a random number generator), and choose where in the subintervals f will be evaluated. Press the "Calculate" button to show the rectangles corresponding to the Riemann sum and to show the value of the Riemann sum.
Back to the Protas home page