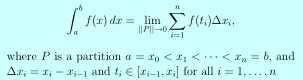
The definite integral can be defined as a limit of Riemann sums.
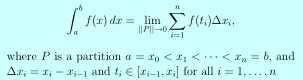
In the applet below, enter the function f(x) and the endpoints of the interval [a,b] over which you want to work. You can use +, -, *, /, ^, (), sin(), cos(), tan(), ln(), log(), asin(), acos(), atan(), pi, e. Take care to remember the * in all multiplications and to avoid discontinuities. Pressing the "Plot" button will draw the graph of f(x). Then enter the number n of subintervals that [a,b] will be partitioned into, choose whether the partition will regular (all subintervals of the same length) or irregular (lengths chosen by a random number generator), and choose where in the subintervals f will be evaluated. Press the "Calculate" button to show the rectangles corresponding to the Riemann sum and to show the value of the Riemann sum.
This applet uses a slightly modified version of the expression parser expr written by Darius Bacon.
Back to the Protas home page