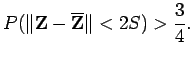Next: Exercises:
Up: notes
Previous: MATLAB and Fourier Transform
The exercises sofar have shown, that it is not easy to distinguish one voice from another using just a sample of one of each of the voices. To resolve these problems we need to look at larger samples an averages. To start use the two voice samples y1 and y2 which you already have. After computing their Fourier transforms z1 and z2 and truncating these transforms to the same length compute the
average
z=(z1+z2)/2;
Now compare z1, z2 and z3 (the Fourier Transform of your team partners voice) directly to the average as follows:
pdj=abs(z-zj).^2;
nrmj=sqrt(sum(pdj))
where j=1,2,3. Answer the following questions:
- Which of the three values for nrmj is the smallest, which one is the largest.
- Compute
p=abs(z).^2;
nrm=sqrt(sum(p))
and compare the values of nrmj with nrm.
- Would you expect the result of the previous exercises to be better or worse if the number of recordings of your own voice is increased? How many times should your own voice be sampled?
In statistics, we usually use the variance or the standard deviation of a sample. If the sample consists of 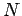 single real valued measurements
single real valued measurements
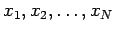 with a
mean
with a
mean
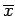 then the standard deviation
then the standard deviation 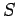 is computed by
Unfortunately, our measurements are neither real valued, nor single numbers, but rather complex valued vectors. This gets us to the following problems:
is computed by
Unfortunately, our measurements are neither real valued, nor single numbers, but rather complex valued vectors. This gets us to the following problems:
- If the sample consists of
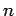 single complex measurements
single complex measurements
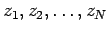 with mean
with mean
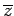 , how should the formula for
, how should the formula for 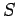 be changed?
be changed?
- If the sample consists of
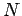 complex vectors
complex vectors
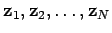 with mean
with mean
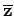 , how should the standard deviation be computed?
, how should the standard deviation be computed?
In order to do statistical testing we need to have an idea, of how your voice samples are distributed. Unfortunately, we do not know that. However, we always have Chebyshev's Inequality. This says that at least 3/4 of all measurements from the same population fall within 2 standard deviations of the mean. Assuming
that
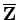 represents your true ``average voice'' and that
represents your true ``average voice'' and that 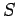 is the
correct standard deviation of your voice, this says that
is the
correct standard deviation of your voice, this says that
for a sample voice 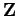 spoken by you. So if a sample voice
spoken by you. So if a sample voice 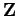 lies outside this ball of radius
lies outside this ball of radius 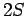 , the probability that it is your own is less that one quarter, and the probability that it is some one else's is greater than three quarters.
, the probability that it is your own is less that one quarter, and the probability that it is some one else's is greater than three quarters.
Subsections



Next: Exercises:
Up: notes
Previous: MATLAB and Fourier Transform
Werner Horn
2006-06-06
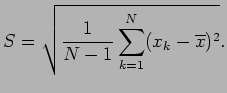
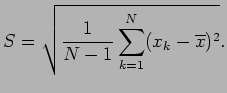
![]() represents your true ``average voice'' and that
represents your true ``average voice'' and that ![]() is the
correct standard deviation of your voice, this says that
is the
correct standard deviation of your voice, this says that