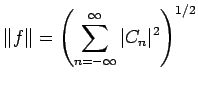Next: Comparing Sounds
Up: notes
Previous: Questions:
From last semesters class we know how to compute the Fourier series of a function 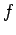 defined on the interval
defined on the interval
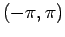 , namely
, namely
and
Fourier series will be the most important tool in this project. In order to use this tool we need to review some of their properties. This will be done by doing some examples. Which you should complete in this work book.
- Let
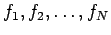 be a finite sequence of
be a finite sequence of 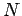 functions with converging Fourier series
functions with converging Fourier series
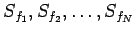 . Prove that
has a converging Fourier series
. Prove that
has a converging Fourier series
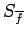 given by
given by
- Suppose that
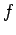 and
and 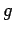 are two continuous functions, such that
are two continuous functions, such that
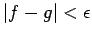 for some
for some
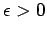 . Let
. Let 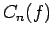 and
and 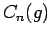 be the Fourier coefficients for these two functions. Prove, that there exists a constant
be the Fourier coefficients for these two functions. Prove, that there exists a constant 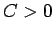 such that
such that
- Suppose that
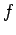 and
and 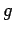 are two continuous functions, such that
are two continuous functions, such that
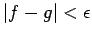 for some
for some
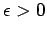 . Let
. Let 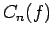 and
and 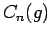 be the Fourier coefficients for these two functions. Prove, that there exists a constant
be the Fourier coefficients for these two functions. Prove, that there exists a constant 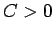 such that
for all
such that
for all 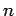 .
.
If functions are defined on a different interval, say ![$ [-L,L]$](img20.png) , we may compute the Fourier series again using some obvious modifications.
, we may compute the Fourier series again using some obvious modifications.
- Write down the equations for the Fourier coefficients and the Fourier series in this situation.
- Restate the statements of number 2 and number 3 above in this changed situation.
In order to compare two sound signals, we need to be able to measure their difference. This leads to the concept of norms.
To become more familiar with this concept you need to complete the following
exercises:
- Let
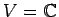 . Show that the absolute value satisfies the requirements of a norm.
. Show that the absolute value satisfies the requirements of a norm.
- Let
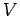 be the set of all continuous functions on
be the set of all continuous functions on
![$ [-\pi,\pi]$](img31.png) . For
. For 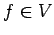 , let
Show that this is a norm.
, let
Show that this is a norm.
- Let
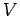 be the set of all continuous functions on
be the set of all continuous functions on
![$ [-\pi,\pi]$](img31.png) . For
. For 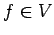 , let
Show that this is a norm.
, let
Show that this is a norm.
- Let
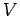 be the set of all continuous functions on
be the set of all continuous functions on
![$ [-\pi,\pi]$](img31.png) . For
. For 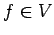 , let
Show that this is a norm.
, let
Show that this is a norm.



Next: Comparing Sounds
Up: notes
Previous: Questions:
Werner Horn
2006-06-06
![]() defined on the interval
defined on the interval
![]() , namely
, namely
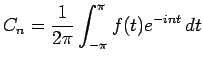
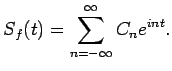
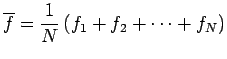
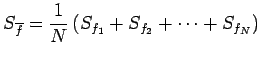
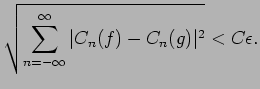
![]() , we may compute the Fourier series again using some obvious modifications.
, we may compute the Fourier series again using some obvious modifications.