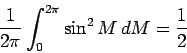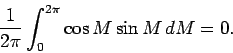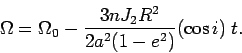Next: About this document ...
Up: master
Previous: Gravity fields and
The motion of the node is described by changes in the angular
momentum vector 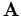 . We derived
. We derived
Only the noncentral part of 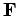 needs to be computed. This means
that we need only
needs to be computed. This means
that we need only
when we compute the perturbations in 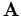 . The corresponding
force is
. The corresponding
force is
Observe that we only have to keep the noncentral part of this,
i.e.,
which gives
In particular, as expected, the  component of
component of 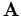 is
conserved.
is
conserved.
For the sake of simplicity, we compute the secular change in the
node only for circular orbits, but for arbitrary
inclination. In this case, we can choose a coordinate system in
which the ascending node is on the positive 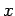 axis. We then have
axis. We then have
where
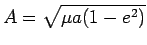 .
.
Consider a coordinate system
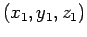 attached to the
orbital plane. In this,
attached to the
orbital plane. In this,
where we can measure the mean anomaly 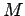 from any point. We
transform the orbit into the original frame by rotation around the
from any point. We
transform the orbit into the original frame by rotation around the
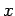 axis and get
axis and get
Then, we have
and
Since for a circular orbit 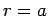 , we have to compute, in
essence, only
, we have to compute, in
essence, only
and
We collect our results to get
and
Hence, the derivative of 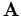 is perpendicular to
is perpendicular to 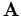 and it is
in the
and it is
in the 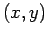 plane. The radius of the circle traversed by
plane. The radius of the circle traversed by 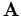 (as the node changes) is
(as the node changes) is 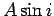 . Hence, the secular change in
the node is
. Hence, the secular change in
the node is
As before, we can use the mean motion to write this as
Of course, since we took 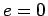 as our reference orbit, this is
valid only for
as our reference orbit, this is
valid only for 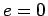 .
.



Next: About this document ...
Up: master
Previous: Gravity fields and
Werner Horn
2006-06-06
![]() . We derived
. We derived
![]() axis. We then have
axis. We then have
![]() attached to the
orbital plane. In this,
attached to the
orbital plane. In this,