Coordinate Transformations

Orbital elements offer an excellent means of keeping track of earth orbiting satellites. However, in order to find the satellite in the sky ant any given time, these elements need to be transformed into a Cartesian coordinate system. his transformation is relatively simple once we can understand the motion of the satellite geometrically. To start with the satellite moves in a plane which goes through the center of the earth. The direction of this plane is determined by three angles, the argument of thw perigee $\omega$, the right ascension of the node $\Omega$, and the angle of inclination $i$.We start with a Cartesian coordinate system with coordinates $(x''',y''',z''')$ in which the $x'''$-coordinate is along the semi-major axis of the ellipse pointing toward the perigee, the $y'''$-coordinate is perpendicular to the $x'''$ axis in the plane of motion, and the $z'''$- coordinate is normal to this plane. The origin is fixed at the center of the earth. Using Kepler's equation we get the eccentric anomaly $E$ from the mean anomaly $f$, and can give the Cartesian coordinates of the satellite in the coordinate system $(x''',y''',z''')$:

$$\begin{eqnarray*} x''' &=& a\cos E-ae\\ y''' &=& b\sin E\\ z''' &=& 0 \end{eqnarray*}$$

In the next step we transform these Cartesian coordinates into a new Cartesian coordinate system $(x'',y''',z'')$, where $x''$ is along the ascending node, $y''$ is perpendicular to $x''$ in the plane perpendicular to the axis of the earth, and $z''$ is along the $z'''$ axis. This is a simple rotation about the $z''$ axis by the negative angle of the right ascension of the perigee $\omega$. It is clear, that $z'''=z''$. For the $x''$ and $y''$ coordinates, a little trigonometry (see Figure x, below) gives:

$$\begin{eqnarray*} x'' &=& x'''\cos\omega -y'''\sin\omega\\ y'' &=& x'''\sin\omega +y'''\cos\omega \end{eqnarray*}$$

Figure 4: Rotation of Coordinate systems

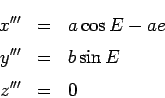
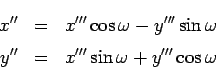
We can make this more efficient by describing it via the rotation matrix

$$A_z(-\omega)=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & \c... ...in\omega\\ 0 & \sin\omega& \cos\omega \end{array} \right]$$

If introduce the notation $X'''=(x''',y''',z''')$ and $X''=(x'',y'',z'')$, we can write the coordinate transformation as

$$X''=A_z(-\omega)X'''.$$

In linear algebra, one studies these rotation matrices in detail. A rotation by an angle $\phi$ about the $x$-axis is given by

$$A_x(\phi)=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & \cos\... ... \sin\phi\\ 0 & -\sin\phi & \cos\phi \end{array} \right],$$

If the rotation is about the $y$-axis the matrix is

$$A_y(\phi)=\left[\begin{array}{ccc} \cos\phi & 0 &\sin\phi... ...0 & 1 & 0\\ -\sin\phi & 0 &\cos\phi \end{array} \right],$$

and a similar formula holds for a rotation about the $z$-axis.

To continue our coordinate transformation we need to rotate the $(x'',y'',z'')$ system about the $x''$-axis (which is also the line of nodes) by an angle of $-i$, this will give us the coordinates $X'=(x',y',z')$ in a Cartesian coordinate system in which the $z'$ axis is along the axis of the earth and the $x'$ axis is along the line of nodes. Following our discussion above this transformation is given by

$$X'=A_x(-i)X'',$$

where

$$A_x(-i)=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0& \cos i & -\sin i\\ 0 & \sin i & \cos i \end{array} \right]$$

The final step is to rotate the $(x',y',z')$ system about the $z'$-axis by an angle of $-\Omega$, this will give us the desired coordinates $X=(x,y,z)$ in the Cartesian coordinate system, in which the $x$-axis points to the vernal equinox. This transformation is again given by a matrix in particular it is given by

$$X=A_z(-\Omega)X',$$

where

$$A_z(-\Omega)= \left[\begin{array}{ccc} \cos\Omega & -\sin... ...in\Omega & \cos\Omega & 0\\ 0 & 0 & 1 \end{array} \right]$$

. We can now combine these three rotations into a single matrix $A_{z'',x,z}(-\omega,-i,-\Omega)= A_z(-\Omega)A_x(-i)A_z(-\omega)$, where the product on the right is the usual matrix multiplication. The coordinate transformation is now:

$$X=A_{z'',x,z}(-\omega,-i,-\Omega)X'''.$$

While this is an elegant way of writing the process down mathematically, in practice it is easier doing the three steps one at a time.