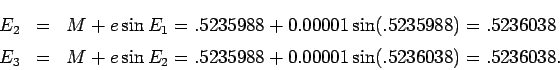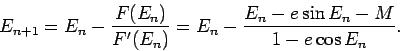Since the mean anomaly is proportional to time it is an easily measured quantity
for an orbiting body. However, in order to compute the location of this body we need to find either the eccentric or the true anomaly. For this one needs to solve Kepler's equation for ![]() . Since this is a transcendental equation, the solution can normally not be found in closed form. However, for small
. Since this is a transcendental equation, the solution can normally not be found in closed form. However, for small ![]() we can devise a simple iteration scheme. To start we rewrite Kepler's equation as
we can devise a simple iteration scheme. To start we rewrite Kepler's equation as
![\begin{Theorem}
Let $f:[a,b]\to [a,b]$\ be a differentiable function such that ...
...\le M l^n
\end{displaymath}
for all $n$\ and some constant $M$.
\end{Theorem}](img186.png)
For a proof of this theorem we refer to a Calculus textbook. Kepler's equation perfectly fits mold of this theorem. First of all, the function ![]() in
(28) satisfies
in
(28) satisfies
Example: A satellite moves on an elliptic orbit with ellipticity
![]() . The mean anomaly is
. The mean anomaly is ![]() , Find an approximate value of the eccentric anomaly. In this case
, Find an approximate value of the eccentric anomaly. In this case
![]() . We set
. We set ![]() .
Using the iteration we get
.
Using the iteration we get