


Next: Kepler's Equation
Up: Kepler's Equation
Previous: Kepler's Equation
In the last section we showed that the orbits are ellipses
following the equation
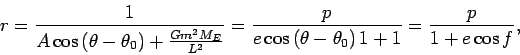 |
(21) |
In this equation 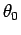 is the angle of the semi-major axes
with the ordinate,
is the angle of the semi-major axes
with the ordinate,
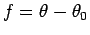 is called the true
anomaly. The angle
is called the true
anomaly. The angle 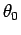 is also commonly denoted by
is also commonly denoted by 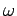 .
One focus sits at the origin of the coordinate system.
The earth is presumed to be at this focus. The perigee is the
point on the ellipse closest to this focus, the apogee, the point
which is farthest. The true anomaly is the angle between a point
on the ellipse and the perigee. Often
.
One focus sits at the origin of the coordinate system.
The earth is presumed to be at this focus. The perigee is the
point on the ellipse closest to this focus, the apogee, the point
which is farthest. The true anomaly is the angle between a point
on the ellipse and the perigee. Often 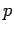 is replaced by
is replaced by
where 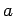 is the semi-major and
is the semi-major and 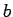 the semi-minor axis.
the semi-minor axis.
It is often more useful to consider an ellipse in a coordinate
system whose origin is at the center of the ellipse. The
eccentric anomaly of a point 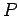 on the ellipse is the angle
on the ellipse is the angle 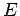 shown in the picture below.
shown in the picture below.
Figure 2:
The relation between the true anomaly 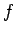 and the eccentric anomaly
and the eccentric anomaly 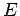
![\includegraphics[scale=0.5]{kepler.eps}](img143.png) |
We will next derive the connections between true anomaly and
eccentric anomaly. Either angle can be used to describe the
properties of an ellipse.
In the above illustration, the point 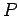 has coordinates
has coordinates 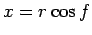 and
and 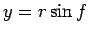 , where
, where 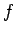 is the true anomaly. The distance
between the center
is the true anomaly. The distance
between the center 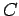 and the focus
and the focus 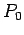 is given by
is given by
Therefore, the 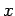 -coordinate of the center is
-coordinate of the center is 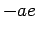 .
The
.
The 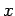 -coordinate of the point
-coordinate of the point 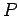 can be computed using
can be computed using 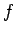 or
or
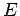 to get:
to get:
For the 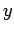 -coordinate we observe:
-coordinate we observe:
i.e.
To continue we see that
Hence,
To continue, we apply the double angle formula in the equation for
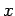 to get
to get
Combining this with the equation for 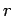 in terms of
in terms of 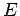 we get
we get
In the same way we get
Combining these we have
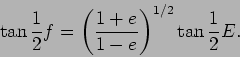 |
(22) |
A relation between the true and the eccentric anomaly.
The final angular measure to compute is the mean anomaly
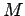 . To do this we note that the satellite does not move with a
constant angular velocity. If it were moving at a constant
velocity
. To do this we note that the satellite does not move with a
constant angular velocity. If it were moving at a constant
velocity 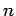 then
then
Assuming that 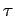 is the time at which the satellite moves
through the perigee, the mean anomaly at time
is the time at which the satellite moves
through the perigee, the mean anomaly at time 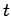 is the angle
is the angle
The mean anomaly is specifically nice since it is a geometric quantity which is directly
proportional to the time. To get the position of the satellite at
a given time we need to compute either the eccentric or the true
anomaly from the time. This relationship is called Kepler's
equation.



Next: Kepler's Equation
Up: Kepler's Equation
Previous: Kepler's Equation
Werner Horn
2006-06-06
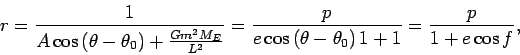
![]() on the ellipse is the angle
on the ellipse is the angle ![]() shown in the picture below.
shown in the picture below.
![]() has coordinates
has coordinates ![]() and
and ![]() , where
, where ![]() is the true anomaly. The distance
between the center
is the true anomaly. The distance
between the center ![]() and the focus
and the focus ![]() is given by
is given by
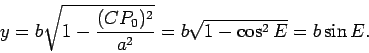
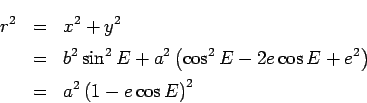
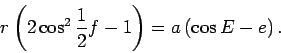
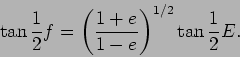
![]() . To do this we note that the satellite does not move with a
constant angular velocity. If it were moving at a constant
velocity
. To do this we note that the satellite does not move with a
constant angular velocity. If it were moving at a constant
velocity ![]() then
then