MATH
310 FINAL EXAMINATION SAMPLE QUESTIONS
|
1. |
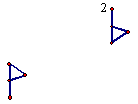
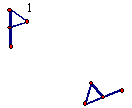
Carefully draw (use a straightedge) each of the following examples. a. Two triangles, DABC
and DDEF,
where b. Two triangles, DABC and DDEF,
where |
|
2. |
Explain why the two triangles in the figure are similar triangles.
|
|
3. |
A person 122 cm tall casts a 37-cm shadow at the same time a tree casts a 148-cm shadow. How tall is the tree? |
|
4. |
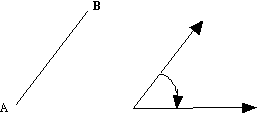
Draw the altitude (height) of the triangle if a. side a is the base b. side b is the base c. side c is the base |
Polygons
|
5. |
Explain, using complete sentences, why a square is both a rhombus and a rectangle. |
|
6. |
a. Sketch and name two nonsimilar polygons with congruent corresponding angles. b. Sketch and name two nonsimilar polygons with a constant ratio of corresponding sides. |
|
7. |
Fill in each blank with the correct word or number. a. The smallest possible number of sides of a concave polygon is _____ b. The number of regular convex polyhedra (Platonic Solids) with triangular faces is ____________ c. The measure of each interior angle of a regular 24-gon is __________ |
|
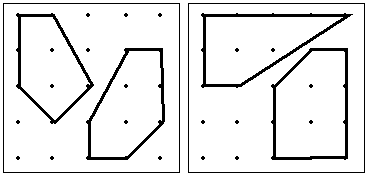
8. |
Show how the geoboard figures can be partitioned into right triangles and rectangles. |
|
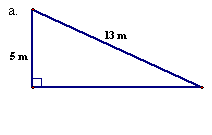
9. |
If the exterior angles of a regular polygon are 22.5° each, how many sides does the polygon have? |
|
10. |
Draw two polygons (with vertices on the lattice points) that each have perimeter 8, but with different areas. Give area of each. |
|
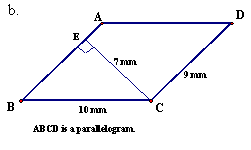
11. |
Find the angle a in each figure below without using a protractor. Figures (a) and (b) are regular polygons and figure (c) is a regular pentagram (hint: the figure formed in the center is regular, and the outer triangles are isosceles). a. b. c.
|
|
12. |
Define each figure given below fully and make a sketch of a typical example. (A definition may be based on any previous definition.) You may assume that "polygon" has been defined previously. a. quadrilateral b. trapezoid c. kite d. rhombus e. parallelogram f. rectangle |
|
|
|
|
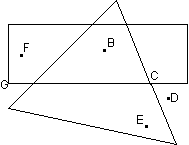
13. |
The figure shows a large triangle intersecting a rectangle.
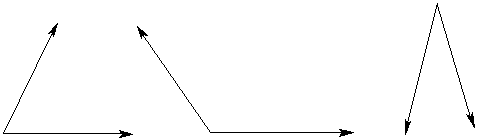
Of the lettered points, name all points that are a. on the rectangle but not on the triangle. b. both in the exterior of the triangle and in the interior of the rectangle. c. on both the triangle and the rectangle |
|
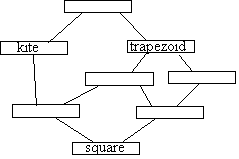
14. |
Place the following in the empty boxes below to show the relationship among the terms. isosceles trapezoid parallelogram quadrilateral rectangle rhombus
|
Lines Parallelism
|
15. |
Classify the following as true or false. a. Two distinct lines can have no more than one point in common. b. Two skew lines determine one and only one plane. c. If a plane contains one point of a line, then it must contain the entire line. d. A ray contains an endpoint. |
|
16. |
If the non-base angle of an isosceles triangle has a measure of 68˚, what is the measure of each base angle? |
|
17. |
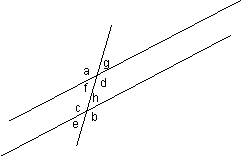
Use the given figure to name a. all pairs of corresponding angles b. all pairs of vertical angles c. all pairs of alternate interior angles d. all pairs of alternate exterior angles |
|
18. |
In each of the following statements place the word “always”, or “never” or “sometimes” in the blank to best complete the statement.. Explain your answer and give appropriate examples to support or illustrate your statement.
|
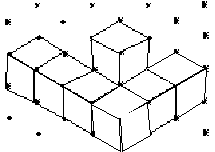
Measurement
|
19. |
Measure each angle to the nearest degree with a protractor.
|
|
20. |
Find the measure of each angle without using a protractor. Show how you got your answer. a. b. c. d.
|
|
21. |
a. Sketch and name two adjacent angles that are complementary. |
|
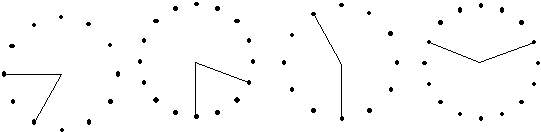
|
b. If the measure of an angle is 13˚ 26' 49", what is the measure of its supplement? |
|
|
c. If (5x)˚ and (7x - 12)˚ are the measures for supplementary angles, what is the measure of each angle? |
|
22. |
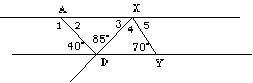
If AX || DY, find the measure of each angle: a) Š1 b) Š2 c) Š3 d) Š4 e) Š5
|
|
23. |
Lani has a photo that measures 3 inches by 5 inches. She wants to enlarge it so that the shorter side measures 4.5 inches.
|
|
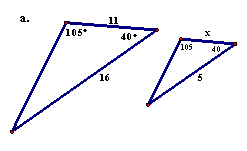
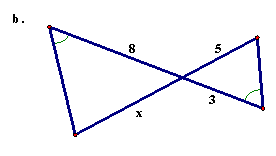
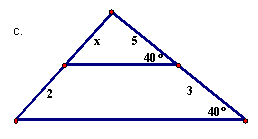
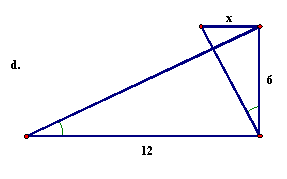
24. |
For each of the following pairs of similar triangles, find the missing measure (side marked x).
|
|
24 |
(continued)
|
|
25. |
What metric system unit would be most appropriate for measuring each of the following? You may use abbreviations for the units. c. The distance from LA to Seattle d. The measure of your waist e. The length of the hallway in a school f. The mass of a box of cereal |
|
26. |
Draw two triangles (with vertices on the lattice points given) that have the same area, but different perimeters. Give the area & perimeter of each. |
|
27. |
For each of the following choose the appropriate metric unit: millimeter, centimeter, meter or kilometer. a. The thickness of a dime b. The length of a straw c. The diameter of a penny d. The distance the winner travels at the Daytona 500. e. The height of a door f. The length of a football field |
|
28. |
Find the area of each of the following.
|
|
29. |
Find the area of the shaded region on the following geoboard if the unit of measurement is 1 square centimeter.
|
|
30. |
Is it possible for a square to have area 11 square centimeters ? Explain why or why not. |
|
31. |
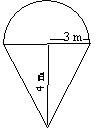
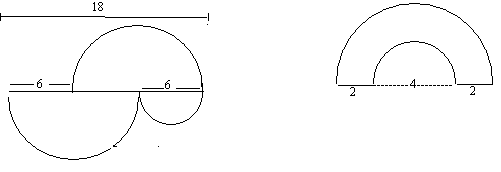
What is the area of the figure below? The arc is a semicircle.
|
|
32. |
For each of the following, can the measures represent sides of a right triangle? Explain your answers. a. 6 m, 8 m, 10 m b. |
|
33. |
Complete each of the following. a. 500 cm2 = _________m2 b. 81 km =_________m c. 4738 g =_________kg d. 300 mL =_________L e. 17 m =_________cm f. 0.10222 kL =_________mL g. 0.027 L = _________cm3 |
|
34. |
If the diameter of a circle is 14 cm, find each of the following. a. The circumference of the circle b. The area of the circle c. The area of a sector of the circle that corresponds to a central angle of 18°. |
|
35. |
Find the perimeters of each of the following if all arcs shown are semicircles. The measurements are in cm. a. b.
|
|
36. |
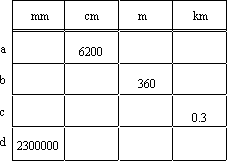
Complete the following table converting metric measures. |
|
37. |
a. Find the complement of 18° 57’. b. Find the supplement of 39° 13’ 28” |
|
38. |
A quadrilateral has area 14 cm2 and perimeter 17 cm . A similar quadrilateral is created that increases the area to 56 cm2. a. What is the scale factor? b. What is the new perimeter?
|
|
39. |
For each, give a value that fits the expression. a. 75% as long as 24 cm. b. 125% more than 24 cm. |
Constructions
|
40. |
Construct each of the following using compass and straightedge. a. Angle bisector of ŠA
b. Perpendicular bisector of segment AB.
|
|
40. |
(continued) c. Altitude of ∆ABC from A
|
|
|
d. Line parallel to l through M
|
Curves
|
41. |
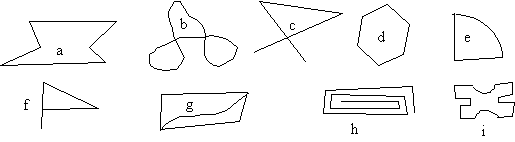
List each figure, a-i, that is a simple curve. List the closed curves. Which of the simple closed curves are convex? Which are polygons?
|
|
|||
|
42. |
Determine whether each of the following is true or false. If false, explain why. a. A diameter of a circle is a chord of the circle. b. A chord may be a tangent of the circle. c. If a radius is perpendicular to a chord, the radius bisects the chord. d. A sphere may intersect a plane in a circle. |
|
|||
|
43. |
a.
Shade in a sector. |
b.
Shade in a segment. |
c.
Draw a central angle. |
d.
Draw an inscribed angle. |
|
Rigid Motions
|
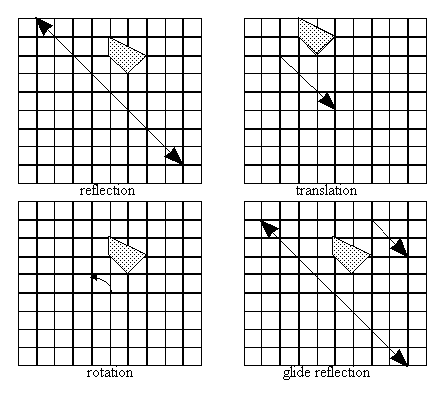
44. |
The two figures in each part are congruent. For each pair, name all possible single transformations that could move figure 1 onto figure 2. a. b. c.
1 2 |
|
45. |
For each of the following transformations, carefully draw the image of segment AB after a. a reflection in line l b. a translation that takes M to N
|
|
|
c. the indicated rotation
|
|
46. |
Describe objects that have each of the following types of symmetry (one object for each of a – d). Make a careful sketch or give the exact name of each object. a. exactly one line of symmetry b. rotational symmetry but not line symmetry c. 45° rotational symmetry d. exactly two lines of symmetry |
|
47. |
For each of the following pairs of figures, determine which single-step transformation might take one figure to the other. Describe the transformation completely. If a rotation, find the center. If a reflection, give the line. If a translation, give an arrow. a. b. c.
|
|
48. |
If possible, describe a geometric figure that can be transformed into itself by each of the following. a. reflection b. rotation c. translation d. glide reflection |
|
49. |
Complete each of the following motions. |
|
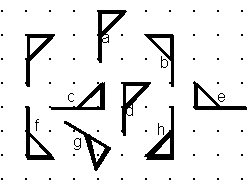
50. |
The unlabeled figure at top left is the original figure. Each of the others, labeled a-g, is the result of a single rigid transformation of the original. Determine if each is the result of a translation, rotation, or reflection.
|
Symmetry
|
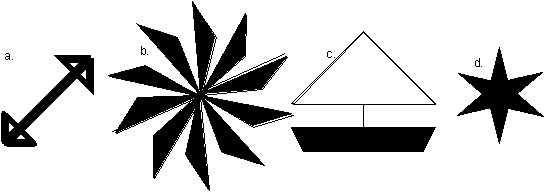
51. |
a. Add to the figure so that it has line symmetry and no rotational symmetry. |
b. Add to the figure so that it has rotational symmetry and no line symmetry.
|
|
52. |
How many lines of symmetry, if any, does each of the following figures appear to have? Draw each line. a. b.
|
|
|
53. |
i) For each figure, give the number of apparent lines of reflection ii) For each figure, give the number of apparent rotational symmetries, including the full turn. |
|
Polyhedra & Solid Figures
|
54. |
a. How many Platonic solids are made with triangles? b. Which Platonic solid is a prism? c. Which Platonic solid is a pyramid? |
|
55. |
Give the complete name of the polyhedron formed by each net. a. b.
|
|
56. |
a. Draw an arrangement of six congruent squares to form a net for a cube. b. Carefully draw a net for a regular tetrahedron. Use a straightedge |
|
57. |
Give a geometric name to the shape of each of these common items. Use adjectives if possible. a. a can of tuna b. a tennis ball c. half an orange d. a box of cereal e. a penny |
|
58. |
What is the least number of faces that a polyhedron can have? |
|
59. |
Sketch a heptagonal prism and show that Euler's formula holds for it. |
|
60. |
a) If a prism has a regular 14-gon for a base, how many faces does it have? b) If a pyramid has 13 faces, how many vertices does it have? c) Is it possible for a prism to have 8 edges? Explain. |
|
61. |
Find the surface area of the square prism having height 6 cm and a base with a side of length 4 cm. |
|
62. |
Answer the following. a. If the volume of a sphere is m3, what is the radius? b. Find the volume of a cylinder whose height is 2m and whose base has a radius of 3 m. Round answer to nearest 0.1 cubic meter. c. Find the height of a square pyramid whose base has side 5 cm and whose volume is 75 cubic centimeters. |
|
63. |
One edge of a cubic tank is 7 m long and the tank is filled with water at 4˚ C; a. Find the volume of the tank in cubic meters. b. Find the capacity of the tank of (a) in liters. c. Find the mass of the water of (a) in kilograms. |
|
64. |
Complete each of the following. a. 3 cubic decimeters of water at 4°C has a mass of ______ g. b. 2 L of water at 4°C has a mass of ______ g. c. 13 cc of water at 4° C has a mass of ______ g. d. 4.2 L of water at 4°C has a mass of ______ g. |
|
65. |
Find the volume of a right circular cone whose slant height is 50 cm and whose height is 0.4 m. |
|
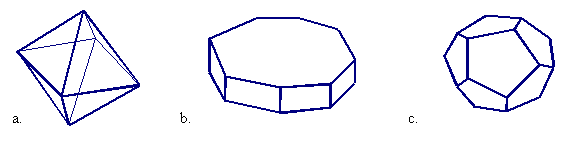
66. |
Write the name of each solid illustrated below. Be as precise as possible.
|
|
67. |
Explain why a pyramid cannot have 19 edges. |
|
68. |
A rectangular pyramid has volume 24 cm3. It is decreased in size by a scale factor of 0.5. What will be the volume of the smaller pyramid? |
|
69. |
a. What is the volume of the figure? b. Carefully draw a top view. |
STATISTICS
|
70. |
Claude paid $38.80 for dinner for himself and two friends. If one friend's meal cost twice as much as Claude's and Claude's meal cost the same as his other friend, answer the following: a. What is the mean cost of the meals? b. What is the median cost of the meals? c. What is the modal cost of the meals? |
|
71. |
Find the mean, median, mode, and range of the following scores. 98 98 98 98 45 84 84 52 45 37 |
|
72. |
The budget for the Women's Center is $1,000,000. If $500,000 is spent on advertising, $150,000 is spent on conferences, and the remainder is spent on long-term securities, construct a circle graph to indicate how the money is spent. Give the central angle for each sector. |
|
73. |
The following are the weights in kilograms to the nearest tenth of Ms. Brown's class. Construct a stem and leaf plot for the data with the stem defined to be all digits to the left of the decimal point. 28.3 27.3 25.6 29.0 27.4 22.7 21.9 22.4 23.7 20.9 21.5 20.1 24.1 21.2 21.9 26.4 23.5 22.5 26.4 23.6 30.1 28.7 27.5 24.6 28.2 |
|
74. |
Twenty test scores are shown below. 31 30 23 27 19 26 28 38 17 29 26 34 21 32 32 22 12 26 39 25 a. Make a grouped frequency table for these scores, using 12-16 for the first class and making a total of six classes of equal width. b. Draw a histogram for the grouped data. |
|
75. |
The mean age of 5 persons in a room is 30 years. A 36-year-old person walks in. What is the mean age of the persons in the room now? |
|
76. |
Mrs. Jurado's class of 20 students averaged 75 on a standardized reading test. Miss Johnson's class of 25 students averaged 66. What is the mean of the two classes combined? |
|
77. |
Mr. E. Z. Grader added 10 points to all the scores on the last exam. The original mean was 72 and the standard deviation 7. What is the mean now? What is the standard deviation now? |
|
78. |
The quiz scores for Mr. Read and Miss Sol's classes are given below. a. Draw a back-to-back stem and leaf plot for the two classes. b. Give the interquartile range for each set of scores. c. Are there any outliers for either set of data? If yes, what are they? d. Draw box plots to compare the two sets of data. e. What is Q1 for Mr. Read’s class? f. What is Q3 for Miss Sol’s class? Mr. Read Miss Sol 72 76 90 85 96 92 90 92 93 78 84 96 78 89 80 92 78 75 88 90 92 83 58 98 |
|
79. |
Find the standard deviation of the set of numbers given below. 5, 18, 12, 6, 7, 3, 15, 10 |
|
80. |
Place 10 points on a scatterplot to illustrate a negative correlation. |
|
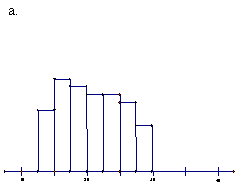
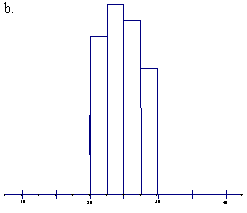
81. |
Which data distribution appears to have the greater standard deviation?
|
|
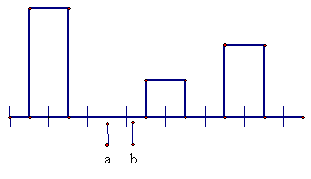
82. |
Considering the mean as a balance point, which point is more likely to be the mean in this line plot, a or b?
|




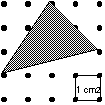





 .
.