Telescopes
Objective:
This activity will introduce telescopes and the use of a virtual telescope. Various astronomical objects will be viewed with our virtual telescope.
Background:
To study and observe astronomical objects astronomers employ telescopes. A telescope magnifies and brightens distant objects using mirrors and lenses.
The two main categories of telescopes are refracting and reflecting. Refracting telescopes (Figure 1) use a lens as the primary light collector and reflecting telescopes (Figure 2) use a mirror. Some telescopes use combinations of both a lens and a mirror.
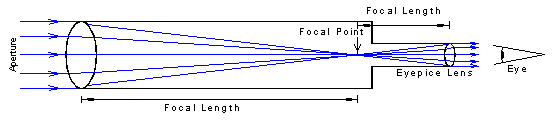
A Refracting Telescope
Figure 1
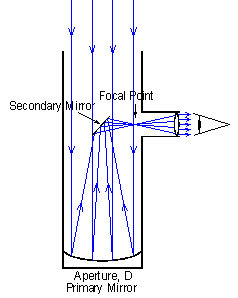
The function of the primary optics is to collect light. The bigger the mirror or lens the fainter the stars that can be detected. Also, the bigger the primary mirror the better the ability of the telescope to resolve fine detail.
A Reflecting
Telescope
Figure 2
Here at CSUN in our campus dome we have a 14” reflecting telescope. The primary mirror is 14” in diameter. The telescope is mounted on a robotic drive system that is interfaced to the Sky Software. All one has to do is click on an object and the telescope will automatically move to the object.

Basic
Properties of Telescopes
1. LIGHT GATHERING POWER
The most important property of a telescope is the ability to gather and collect light. We call this the light gathering power. The amount of light that a telescope gathers depends on the area of the opening of the telescope through which light passes. Most telescopes are described by the diameter of their openings. The light gathering power increases as the square of this diameter. Therefore, a telescope with twice the diameter will have four times the light gathering power.
We can compare the light gathering power of any telescope to that of the human eye. The human eye, when fully dilated has a diameter of about 1/4 of an inch. Therefore, the light gathering power of a telescope with a diameter of D inches would be given by:
LGP = (D*4)2
For example, CSUN’s 14 inch telescope would have (14*4)2 = 3136 times more light gathering power than the human eye!
2. ANGULAR RESOLUTION
The ability of a telescope to reveal fine detail depends on its resolution. The angular resolution of a telescope determines the least amount of angular separation required to be able to view two objects distinctly. Any closer and the two objects would blur together and appear as one object. When speaking of telescopes, the separations considered are such small angles that they are measured in seconds of arc. The limits of resolution are caused by a natural phenomenon of light called diffraction. The larger the opening the closer two objects can be placed and still be distinguished. Given the diameter D in inches, we can estimate the theoretical angular resolution of a telescope to be
R = 4.8/D seconds of arc
For example, the angular resolution of CSUN’s 14 inch telescope is (4.8/14) = 0.34”. If the two stars we are viewing are separated by 0.5”, then our telescope would be able to distinguish both stars. If, however, the two stars we are viewing are only separated by 0.2”, we would only see one object through our telescope.
SEEING LIMIT
The above calculation involves a theoretical resolution. In reality, ground based telescopes are affected by the atmosphere. Even with the most ideal weather for viewing, turbulence in the upper atmosphere still reduces a telescopes ability to resolve images. The practical limit of resolution for telescopes on the earth is about 0.5” regardless of the diameter. This can be overcome by placing telescopes in orbit or by using an adaptive optics system.
3. MAGNIFICATION
The magnification of a telescope is how much larger an object appears when viewed through the telescope than when viewed with the naked eye. We calculate this by dividing the focal length of the objective by the focal length of the eyepiece.
MAG = fo / fe
This is the least important factor to consider when choosing a telescope as it can be adjusted by changing the eyepiece, so almost any magnification can be obtained. However, the size of the telescope places practical limits on the magnifications that can be used.
a. MAXIMUM MAGNIFICATION
Because of the limits of resolution there’s only so much detail that can be seen with any given telescope, no matter how large the image. The practical maximum limit of the magnification of a telescope can be approximated by multiplying the diameter of the telescope (in inches) by 50. For example, CSUN’s 14 inch telescope can be used to magnify objects up to (14x50) = 700x. Beyond this, the images would simply be large, blurry, and of no use.
b. MINIMUM MAGNIFICATION
We call the cone of light that comes out of the eyepiece the exit pupil. This cone of light then enters our eye and we see an image. The size of the exit pupil is the diameter of the telescope divided by the magnification (EP = D/M) and thus decreases with greater magnification. If the size of the exit pupil is larger than our eye’s dilated pupil, then the extra light will be wasted. We want to use all the light gathered by our telescope (or else why buy a larger telescope?) so we choose a magnification that reduces the exit pupil to the size of our eye pupil. This is approximately 4 times the diameter of the telescope in inches. For example, when viewing with CSUN’s 14 inch telescope, the images should at least be magnified (14x4) = 56x.