What is a complex fraction?
A complex fraction is a fraction with fraction within it. Meaning that both the numerator and the denominator may contain fractions themselves.
Here is an example of a complex fraction:
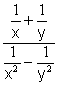
Lecture : Complex Fractions
What is a complex fraction?
A complex fraction is a fraction with fraction within it. Meaning that both the numerator and the denominator may contain fractions themselves.
Here is an example of a complex fraction:
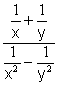
Now that we know what a complex fraction is, we need to learn to simplify them. We simplify complex fractions by following the below steps:
1. We simplify the numerator, meaning that we write it as one fraction.
2. We simplify the denominator, meaning that we write it as one fraction.
3. Now we will have a fraction over a fraction, so we will multiply by the reciprocal of the denominator.
Example:
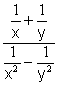
we begin by looking at the numerator, and writing it as a single fraction.
![]()
the lcd will be xy
![]()
Now we have the numerator as a single fraction, we do the same with the denominator.
![]()
the lcd is x2y2
![]()
Now we have both the numerator and the denominator written as single fractions, and our complex fraction looks like this
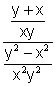
To simplify a fraction divided by a fraction we mulitply by the reciprocal of the denominator, giving us
![]()
Now we are left with a multiplication of rational expressions problem, so we will factor anything we can, and cancel like terms.
Note that x + y is the same as y + x, so those two factors will cancel. We may cancel an x and a y out of both the numerator and the denominator.
![]()
= ![]()
and this is our final answer.
Simplify each of the following complex fractions
1) Simplify ![]() solution
solution
2) Simplify 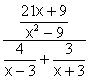 solution
solution
3) Simplify 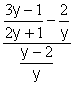 solution
solution
we begin by looking at the numerator, and writing it as a single fraction.
The lcd will be x
![]()
Now we have the numerator as a single fraction, so we do the same with the denominator.
The lcd is x:
![]()
Now we have both the numerator and the denominator written as single fractions, we simplify the complex fraction by dividing the fraction in the numerator by the fraction in the denominator
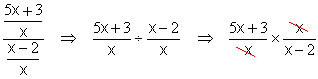
We have nothing which needs to be factored, but x is common to both the numerator and the denominator, so we may cancel it. And our final answer will be:
![]()
Simplify 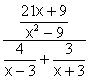
Note in this problem we start out with the numerator as a single fraction, so we may leave it alone, and only we write the denominator as a single fraction.
![]()
the lcd is (x - 3)(x + 3)
![]()
![]()
Now we have both the numerator and the denominator written as single fractions, and our complex fraction looks like this
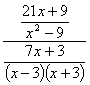
To simplify a fraction divided by a fraction we mulitply by the reciprocal of the denominator.
![]()
To simplify we will factor anything that we can, and cancel like terms.
![]()
So our final answer is 3
Simplify 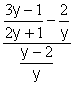
We begin by looking at the numerator, and writing it as a single fraction.
the lcd will be y(2y + 1)
![]()
![]()
Now we have the numerator as a single fraction. When we look at the denominator, we see that it is already written as a single fraction. Since we have both the numerator and the denominator written as single fractions, our complex fraction looks like this
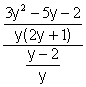
To simplify a fraction divided by a fraction we mulitply by the reciprocal of the denominator. The numerator of the first fraction is a factorable trinomial, so we factor it and cancel the common factors:
![]()
![]()