Notes - Mod. VII - Chapter 1
I. MONOMIAL ARITHMETIC
Addition and Subtraction
When adding or subtracting monomials we combine the numerical parts only if letter parts are the same.
i.e. The only algebraic terms which can be combined are like terms.
Example: Find the sum of 14xyz , 2xy , -3xyz , 4xz , and -5xz
14xyz + 2xy + (-3xyz) + 4xz + (-5xz)
= 14xyz - 3xyz + 4xz - 5xz + 2xy
= 11xyz - xz + 2xy
Example: Subtract -5ab from the sum of 7a2b , 2ab , 3ab2 and -6ab
To avoid errors put -5ab in parenthesis and then subtract as follows :
7a2b + 2ab + 3ab2 + (-6ab) - (-5ab)
= 7a2b + 2ab + 3ab2 - 6ab + 5ab
= 2ab - 6ab + 5ab + 7a2b + 3ab2
= -4ab + 5ab + 7a2b + 3ab2
= ab + 7a2b + 3ab2
Multiplication and Division
The product of monomials will give us another monomial . We multiply the number parts . The letter parts are multiplied by adding the exponents .
Example:
Find the product of 7a2b , abc , 3ab2 and -6a3bd
7a2b ´ abc ´ 3ab2 ´ (-6a3bd)
= 7 ´ 3 ´ (-6) ´ a2 ´ a ´ a ´ a3 ´ b ´ b ´ b2 ´ b ´ c ´ d
= 7 ´ 3 ´ (-6) ´ a2 + 1 +1 +3 ´ b1 + 1 + 2 + 1 ´ c ´ d
= -126a7b5cd
When dividing algebraic expressions we can cancel factors as follows :
Example: Divide 27a2b3c by 9ab2c3
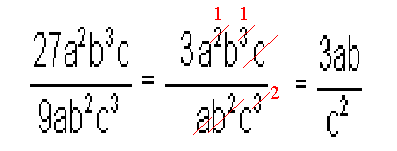
We must be careful with exponents :
Example: 1.True or false (-5)0 = -50
2.True or false 5ab3 = 5(ab)3
Both equations are false .
Solution to # 1 : (-5)0 = 1 while -50 = -1 therefore (-5)0 is not equal to -50 . When -5 is not enclosed in parenthesis the 0 exponent operates only on the 5 and not the negative sign in front of the 5 .
Solution to # 2 : The solution is similar to the solution for #1 . With 5ab3 the 3 exponent operates only on the b . With 5(ab)3 the 3 exponent operates on everything within the parenthesis .