Solids:

Lateral and Total Surface Area:

The Lateral Area of a solids is the area of the faces of the solid that intersect its base. Or in other words the area of the "walls" of the solid.

The Total Surface Area of a solid is the area of all the faces of that solid (Lateral Area + the area of the base(s) ).

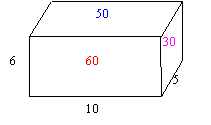
Example 1) Find the Lateral and Total Surface Area of the following solid:
 

The walls of this rectangular prism consist of 4 rectangles. To to find the lateral area we have to find the areas of these rectangles and add them. Notice that the walls the area of the rectangles that are parallel to each other are equal in this solid.
 

L.A. = 60 + 60 + 30 + 30 = 180

T.S.A.= 180 + 50 + 50 = 280

Example 2) Find the Lateral and Total Surface Area of the following solid: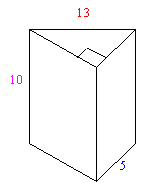
 

The walls surrounding this solid are three rectangles each having height 10. We know the base for two of the rectangles (5 and 13), but the base of the third rectangle is not given. But since the base triangles are given to be right triangles, we can use the Pythagorean theorem to find the missing side.
 

5² + x² = 13²

25 + x² = 169

x² = 144

x =  = 12

Now we can find the area of all three rectangles and add them.
 

L.A. = 12 ´ 10 + 5 ´ 10 + 13 ´ 10

L.A. = 120 + 50 + 130 = 300

To find the Total Surface Area, we have to add the area of the two bases (top and bottom) of this solid to the Lateral Area. Each base is a triangle. Recall that the area of a triangle is found by using the formula A= ½ bh
 

T.S.A.= 300 + ´ 5 ´ 12 + ´ 5 ´ 12

Example 3) Find the Lateral and Total Surface Area of the following solid: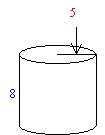
 

To find the lateral area of a cylinder we have to first cut open the lateral wall vertically to make a rectangle and then find the area of the rectangle.
 

The resulting rectangle has height 8 and its length is equal to the circumference (C=2p r) of the circular base.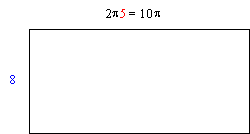

L.A. = (10p ) 8 = 80p

To find the Total Surface Area we have to add the area of the circular bases to the lateral area.
 

T.S.A. = 80 p + p 5^{2 + p} 5²

T.S.A. = 80 p + 25 p + 25p = 130p

The volume of a solid is the number of unit cubes that can fit inside of that solid. In this class we will consider two types of solids: Prisms and Pyramids.

A prism is any solid with two congruent (identical) and parallel faces. The volume of a prism is found by finding the area of one of these faces and multiplying it by the length of the height of the prism (the line perpendicular to the face).
 

A pyramid is a solid with only one base and no parallel faces. The volume of a pyramid is found by multiplying one third area o fate base by the length of the height.
 

Example 4) Find the Volume: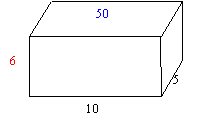
 

The bases of this solid are congruent and parallel. So it is considered a prism. Each rectangle has area 50:
 

V = 50 ´ 6 = 300

Example 5) Find the Volume:
 

The bases of this prism are triangles whose area we found in example 2 to be 30.
 

Example 6) Find the Volume:

A cylinder is considered a prism since the circular bases are parallel.
 

V= (p 5^{2) ´} 8

V = (25p ) ´ 8 = 200

Example 7) Find the Volume:
 

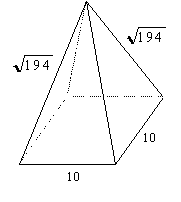
To find the volume of this pyramid we have to find the height of the pyramid (the red line drawn inside of the pyramid). In order to find the length of the slant height of the pyramid (the blue line). This line is the height of the triangle on the surface of the pyramid.
 
 
 

Then we have to use the Pythagorean theorem again in the triangle formed inside of the pyramid by the slant height the base and the height of the pyramid.
 

V = 1/3 (Area of the Base)(H)

V = 1/3 (100)(12)

.