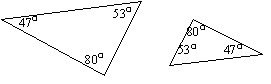
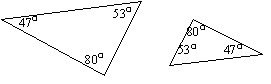
If two triangles are similar then the length of their sides are proportional.
That means that if for example one side of the larger triangle is three
times as long as the corresponding side (across from the same size angle)
of the smaller triangle then all the sides of the larger triangle are three
times as large of their corresponding parts in the smaller triangle. This
fact allows us to find missing parts of similar triangles by setting up
proportions and cross multiplying.
| Refresher on Cross multiplying:
If we have two fractions that are equal to each other we are allowed to multiply the numerator of one fraction with the denominator of the second fraction and set the result equal to the product of the denominator of the first fraction and the numerator of the second fraction. For example: Note that we are only allowed to do this if we have single fractions equal to each other. |
Example 1)
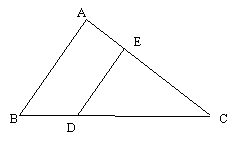 |
Given AB || DE (parallel)
AB = 24 AE = 5 EC = 15 Find DE. |
Since AB and DE are parallel the corresponding angles at the two lines are congruent (<D = <B and <E = < A)
Which means that the triangles ABC and EDC are similar and their sides are proportional. First thing we’ll do is separate the two triangles from each other and write the length of each side next to it. Then set up our proportion and cross multiply.

![]()
20x = (15)(24) ![]() 20x
= 360
20x
= 360 ![]() x
= 18
x
= 18
![]() DE=18.
DE=18.
Copyright © 1997 Bamdad Samii