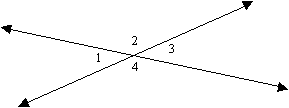
Angles:
Angles are formed as a result of intersecting lines. In fact whenever two lines intersect four angles are formed.
Which we Ill label <1 , <2, <3 and <4.

The measure (size) of these angles are closely related.
|
1. Two angles whose sides are opposite rays of each other are called vertical angles. Vertical angles have the same measure. |
Notice that angles <1 and <3 in the above diagram are formed by opposite rays (are formed by the same two lines, but are across from each other) . This means that <1 and <3 are vertical angles and have the same measure. The same is true about <2 and <4.
|
2. The measure of two adjacent angles that form a straight line add up to 180O. Angles whose measures add up to 180O are called supplementary angles. |
Notice that <1 and <2 are adjacent (share a side) and form a straight line together. This means that their measures add up to 180O . The same is true for <2 and <3, angles <3 and <4, and angles <4 and <1.
|
Example 1) Find X and Y. <Y and the 42O angle are vertical angles so Y=42 and <X and the 42O angle are adjacent angles that form a straight line so their measures must add up to 180O. So X=180 42=138. |
|
Parallel lines
:When two parallel lines are intersected by a third line (a transversal) then 8 angles are formed, 4 at each line .
|
We have already established that <1 and <3 are vertical angles and have the same measure. The same is true for <5 and <7. Now since the lines are parallel we can also establish that all four have the same measure. That is <1 = <3 = <5 = <7. The same can be said for <2, <4 , <6 and <8. These angles will have the same measure. |
|
|
Example 2) Given L1 || L2 , find X. Notice that since the lines are parallel <X is congruent (has the same measure) to the angle adjacent to the 36O so it is supplementary to the 36O angle. X= 180 36 = 144. |
|
Angles in a Triangle:
|
The sum of the measure of the three interior angles in any triangle is 180O. <1 + <2 + <3 =180O |
|
Example 3) Find X.

In order to find X we have to find the interior angle of the triangle that is vertical to it. And to find the measure of that angle we need to find the remaining interior angles of the triangle. We start with the interior angle adjacent to the 135O angle. Since these angles are adjacent and form a straight angle, their measures must add up to 1800, so its measure is 180 135 = 45O.
The interior angle at the top of the triangle and the 64O are vertical angles so they have the same measure.
Now that we have two out of three interior angles we can find the third. 180 45 64 = 71O . Now this angle and <X are vertical angles and have the same measure so X= 71.
Sample Problems:
1)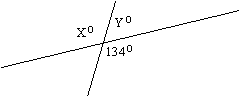
2)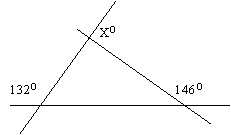
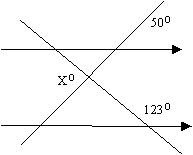
3)
Solutions:
1) X=134 Y=46
2) X=82
3) X= 107O