A ratio is a comparison of two numbers by division. The ratio of a to b is

We can handle ratios as fractions, since a ratio is a fraction, b can never be zero. (). A ratio is number, so if you want to find the ratio of two quantities they must be expressed in the same units.

Example: Wath is the ratio of 8 inches to 6feet?

A proportion is a statement that two ratios are equal. For example, is a proportion; it could also be expressed as 3:12 = 1:4. The proportion a:b = c:d or , is equivalent to the equation ad = bc. Finding the products ad and bc is also called cross-multiplying the proportion: . So cross-multiplying a proportion gives us a way to find a missing number in a proportion.

Example: Find x if Þ Þ divided both sides by 4

In exercises involving proportions , ratios will either be presented as fractions or in the sentences of a word problems . One way of avoiding errors when setting up proportions is to label the ratios . For example, if the ratio of men to women in the class is 4 to 5 and there are 20 men in the class , how many women are in the class ?

We will need to set up an equality of two ratios . The first thing to notice is that our ratios are set up as men to women and then we can fill in the ratios as follows :

Solving this proportion for x (see page 8 in Module IV) we find the number of women in the class is 25 .

With some proportion exercises , labeling the ratios is not so obvious . If there are 35 students in the class and the ratio of men to women is 4 to 3 , how many men are in the class ? We cannot write the ratio 4 / 3 as this is the ratio of men to women. We need to set up the ratio of men to total number of students in the class . One way of solving this exercise is to look at the given 4 to 3 ratio and imagine that there were only 4 men and 3 women in the class . If this were the case, we would have a total of .7 students in the class . That is , the number of men to total number of students would be 4 to 7. To find the total number of men in a class with a total of 35 students we can set up the proportion as follows:

Solving for x we get the total number of men in a class of 35 total students :

Cross-multiply to get :

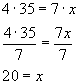
Thus , with x representing the number of men we see there are 20 men in.the class of 35 students .