Multiplication is an operation that associates with each pair of quantities a third quantity called the product. We write st or s(t) or (s)(t) to present the product of s and t. Each of the quantities we multiply is called a factor.

Additional factoring example : for integers 6 and 42 , 6 is a factor of 42 as 6 divides evenly into 42 . 42 has factors other than 6 , for instance 3 is factor of 42 . Note that 3 is also a factor of 6 . Thus if 6 is a factor of 42 then 3 must be a factor of 42 as well .

We can find all the factors of an integer like 72 and we do so in set notation :

then we proceed to fill in the brackets

Practice Problem:

#1 List the factor set of 42. Solution

Recognizing Factors (Module II, page 20)

Is 1254321 divisible by three ? There are some techniques on page 20 of Module II that are quite good for recognizing factors of large numbers .

Practice Problem:

#2 Determine whether or not each of the following are factors of 390?

2, 3, 5, 6, 10, 11, 13, 15, 30.

Solution

Prime Factorization (Module II, page 21)

To find the prime factorization of an integer see steps on bottom of page 21 in Module II

1 is not a prime number . Why ? 51 is a composite number . Why ?

The PRIME FACTOR TREE is a good way to find the prime factorization of a number:

Suppose we needed the prime factors of 48 . We know that 48 ends in an even number , thus 2 divides evenly into 48 . 2 x 24 = 48 so we start our "tree" as follows:

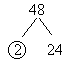
Circle the prime and move on to the composite, 24 in this case . We know that 6 and 8 divide evenly into 24 but I want to stress that you look for the smallest prime that divides into 24. 2 is the smallest prime. 2 ´ 12 = 24 so we continue with:

Thus , 48 = 2 · 2 · 2 · 2 · 3 = 2⁴ · 3 <== this is 48 written in EXPONENTIAL NOTATION .

Practice Problem:

#3 Write 252 as a product of prime numbers. Solution

Solution:

#1 {1, 2, 3, 6, 7, 14, 21, 42}

#2 2, 3, 5, 6, 10, 13, 15, 30 are factors. (Except 11)

#3 252 =

[Go back to]: top