a) Exponential notation is another way to express repeated multiplication. For example, . In general we define exponential notation for a positive integer n as follows.

(n factors )

In this expression, b occurs as a factor n times, b is called the base and n is called the exponent (or power). i.e. base^exponent or base^power

So the exponent tells us how many times to use the base as a factor in an exponential expression.

b) If no exponent is written, it is understood to be one. That is, b means b¹.

c) We define b⁰ = 1, for any real number . So any non-zero number raised to the zero power is one. If b = 0, then 0⁰ = undefined.

Examples:

2⁴ =

Can you tell the difference between this one and

-16

d) From the second and third example, we notice that

Practice Problems:

#1 (-1)¹⁵ = #2 0⁴ = #3 -2⁴ =

#4 (-2)⁴ = #5 747⁰ = #6 x⁰ =

Solution

Consider the following product:

2³ · 2⁵

We recognize that:

2³ = and

2⁵ =

So 2^3· 2⁵ = · = 2^{3 + 5} = 2⁸

In general, b^mbⁿ means m factors of b times n factors of b. There are then m + n factors of b, which may be written as b^m+n. When multiplying two or more expressions with the same base, simply write the base and add the exponents. Thus

Let us consider other expressions that involve exponential factors. Specifically let's discuss (b^m)ⁿ where m and n are natural numbers. The n means to use b^m as a factor n times and the m tells us to use b as a factor m times. Therefore we have

The two basic formulas for problems involving exponents are:

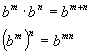
Examples:

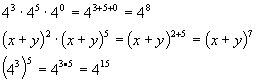
Practice Problems:

#7 #8 #9 #10

Solution

We can write the powers of 10 using exponents. For example:

10⁰ = 1

10¹ = 10

10² = 100

10³ = 1000

10⁴ = 10000

This suggests the relationship between the exponent in the power of ten and the number of zeros in the decimal number for the power; the exponent tells how many zeros occur in the number.

We can use exponents in wrtiing the expanded notation of an integer. For example:

Practice Problem:

#11 Write 98,012 in expanded form using powers of ten.

#12 Write the decimal number indicated by:

Solution

#1 -1

#2 0

#3 -16

#4 16

#5 1

#6 1 ()

#7 5⁸

#8 3²⁰

#9

#10 a⁶

#11

#12 1,058,203

[Go back to]: Top