In solving a system of equations we are trying to find the set of numbers that satisfy all the equations in the given system.
For example if we consider the system: ![]()
There are an infinite number of points that satisfy each equation, but not necessarily both equations. The point (2,8) satisfies the top equation but not the bottom equation, while the point (1,5) satisfies both equations. We say the solution to the above system is (1,5). Considering the problem geometrically (1,5) is the point where graph of the above equations intersect.
There are many methods for finding the solutions to system of equations. We will discuss two methods here: the addition method and the substitution method.
In the addition method our goal is to multiply each equation by an appropriate number in such a way that when the two equations are added one of the variables is cancelled. This would result in an equation with only one variable that we can then solve for. The we will replace the solution in one of the original equation and solve for the remaining variable.
Example 1) Solve: ![]()
We first choose a variable that is easier to eliminate. In this problem there is no difference so we can start by eliminating the x's. In order to do this we have to make sure that the coefficients of x are the same number with different signs. We can achieve this by multiplying the top equation by 5 and the bottom equation by -2. The result will be coefficients of 10 and -10 for the two x's respectively. This allows them to cancel when the two equations are added together.
![]()
Now when we add the two equations together we get:
11y = -11 which gives us y = -1
Now plugging -1 in the top equation (the bottom equation gives us the same answer), we get:
2x + 3(-1) = 1
2x - 3 = 1
2x = 4
x = 2
So the solutions is: (2,-1).
Example 2) Solve: ![]()
Here we have to first reorder the second equation so that the variables line up. We add an x to both sides: ![]()
Now we can try to eliminate the x's by multiplying the top equation by -2:
![]()
Adding these two equations together we get: 0 = -9 which is a contradiction. This means the system has no solution. We say that the system is inconsistent. Considering it geometrically this means that the above graphs do not intersect (the lines are parallel).
Example 3) Solve: ![]()
We can eliminate the x's by multiplying the top equation by - 4:
![]()
Adding the two equations together we get: 0 = 0. This is a true statement (an identity), which means that any point that satisfies the first equation will also satisfy the second equation. In geometrical terms, both equations describe the graph of the same line.
In problems like this we solve one of the equations for y and then write the solutions as (x , mx + b).
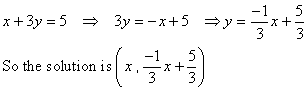
In the substitution method, our goal is to solve one of the equations for a variable and then substitute it in the other equation for every instance of that variable. This method is usually used when one of the equations is already solved for either variable or if we have non-linear equations.
Example 4) Solve ![]()
We start by solving the top equation for x: x = 5 - 2y
Now we substitute this expression for x in the second equation (it is very important that we use the other equation to substitute into - if we substitute into the same equation we will always get an identity):
(5 - 2y)2 + y2 = 5
(5 - 2y) (5 - 2y) + y2 = 5
(25 - 20y + 4y2) +y2 = 5
5y2 - 20y + 25 = 5
This is quadratic equation so we have set it equal to zero:
5y2 - 20y + 20 = 0
5(y2 - 4y + 4) = 0
5(y - 2) (y - 2) = 0
y = 2
And we know that x = 5 - 2y So x = 5 - 2(2) = 5 - 4 = 1.
The solution is (1,2)
Example 5) Solve ![]()
In this problem it is easier to solve the bottom equation for y: y = 8 - 3x
Then substitute it into the top equation: x(8 - 3x) = 4
To solve this equation we have to first distribute the x.
8x - 3x2 = 4
Then we move everything to one side and try to either factor or use the quadratic formula:
0 = 3x2 - 8x + 4
0 = (3x - 2)(x - 2)
x = 2/3 and x = 2
And we can find their corresponding y's by plugging in these values for x:
x = 2/3 then y = 8 - 3(2/3) = 8 - 2 = 6
x = 2 then y = 8 - 3(2) = 8 - 6 = 2
So the solutions are : (2/3,6) and (2,2).