You will want to read Chapter 1 of Module I carefully to gain an understanding and to be able to identify the different categories of Real numbers . Be able to explain the difference between a Natural , Integer, Rational and Irrational number . Are all integers rational ? Are all rational numbers integers ?

You will see a lot of "why" questions in these notes . It is important to answer these questions and to ask more "why" questions of your own as you read .

I. The Real Number System ( Refer to Module I page 3 )

The system of Real Numbers includes Natural numbers , Integers, Rational numbers, and Irrational numbers . Know how to define and give examples of these types of Real numbers .

One thing I want to highlight about irrational numbers is the last sentence in the definition of irrational numbers on page 3 . As an example of an irrational it gives where x is NOT the square of any integer or rational number . This means is not irrational because 25 is the square of 5 . On the other hand is irrational . Why ? Is 17 the square of an integer ?

II. The Real Number Line (see page 5 in Module 1)

All natural , integer, rational and even irrational numbers can be found on the real number line .Locate and on the Real number line. Can you estimate where exists ? Is rational or irrational ? Why or why not ? Is -5 to the left or right of -11 on the real number line ?

To add 7 to a given number is to move to the right ( in the positive direction ) along the number line by 7 (integer) units . To subtract 5 from a given number is to move to the left (negative direction) by five units.

Before discussing these properties I want to stress some definitions . Here-to-fore when you see the term OPERATOR understand that this refers to either addition , subtraction , multiplication or division . Addition is an OPERATOR (or OPERATION ) on two numbers and so is subtraction , multiplication and division . You will want to be familiar with the definitions of SUM , DIFFERENCE, and PRODUCT given in chapter 2 . The QUOTIENT of two numbers is the result after division . For example , 2 is the QUOTIENT of 10 ÷ 5 .

a) Commutative and Associative properties .

We say that addition is commutative because we can add 5 + 2 and get the same result if we add 2 + 5 . Flipping the numbers this way is what it means to commute two numbers . Big deal , right ? But does subtraction work the same way ? How about multiplication and division ? The only way to find out is to try a few numbers . Is it true that 5 - 2 = 2 - 5 ? Does 5 x 2 = 2 x 5 ? Is 5 ÷ 2 = 2 ÷ 5 ?

This is best illustrated in your module on page 19 .

c) Decimal number system .

Why do we call it the decimal number system . There are other number systems . The computer you are on right now does its calculations with the binary (2 characters , just 1 and 0) number system . Do you have a good guess as to why we humans decided that a 10 character number system would be most convenient ?

d) Positional notation is very important !! Look at the number 58,123 . We say the 5 is in the ten-thousands place. The 5 stands for 5 x 10,000 . In Expanded notation we write :

58,123 = (5 x 10,000) + (8 x 1,000) + (1 x 100) + (2 x 10) + (3 x 1).

One of the most common problems I see in this class is disregard for position when doing long division . This leads to a lot of errors . Remember calculators are not allowed during the test so you will want to practice long division . Try the following using long division :

Solution

e) When we say "the set of integers is CLOSED under addition" we are saying that if you add two integers you get another integer . 5 + 7 = 12 , 5 and 7 are both integers and the result after addition is 12 , another integer . The Natural numbers are also closed under addition but they are not closed under subtraction . 5 - 7 = - 2 , 5 and 7 are both natural numbers but -2 is not a natural number (see the definition of natural numbers) . Is the set of integers closed under division ?

 Solution

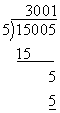
remainder is 13, alternatively we write

.