Modeling a Predator/Prey Population Study

Author(s): Jon Fisher
Growth & Development Experiment
SED 695B; Fall 2005

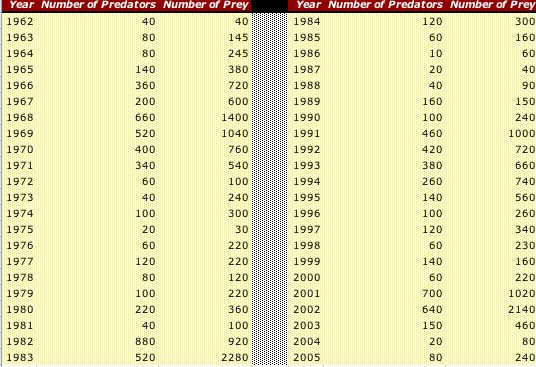
Research Question:

How do populations of predators and prey change over time?

 

Standards addressed:

6th grade science:

5e. Students know the number and types of organisms an ecosystem can support depends on the resources available and on abiotic factors, such as quantities of light and water, a range of temperatures, and soil composition.

Biology

6c. Students know how fluctuations in population size in an ecosystem are determined by the relative rates of birth, immigration, emigration, and death.

6th Grade Math

2.0 Students use data samples of a population and describe the characteristics and limitations of the samples:
2.1 Compare different samples of a population with the data from the entire population and identify a situation in which it makes sense to use a sample.
2.2 Identify different ways of selecting a sample (e.g., convenience sampling, responses to a survey, random sampling) and which method makes a sample more representative for a population.
2.3 Analyze data displays and explain why the way in which the question was asked might have influenced the results obtained and why the way in which the results were displayed might have influenced the conclusions reached.
2.4 Identify data that represent sampling errors and explain why the sample (and the display) might be biased.
2.5 Identify claims based on statistical data and, in simple cases, evaluate the validity of the claims.
Independent variable
Dependent variables
Controls
Series
population of predator and prey   none time
Materials
Procedures
  1. A newspaper with a date written on it*
  2. Colour Pencils
  3. 12 inch ruler
  4. data sheet
  5. graph paper

*the newspapers are pre-sorted and labeled by the teacher to create population flux.

 

 1. Each student will be given a piece of newspaper with a year written on top. A ruler and a colored pencil.
2. In the middle of each newspaper page the student should draw a 10” x 10” grid. This grid will represent the study area (full of mice and hawks) for our hypothetical forest.
3. Label the boxes along the horizontal axis A-J. Label the boxes along the vertical axis 1-10.
4. We have now labeled the grid for our population study.
5. In the study area delineated by the grid, we will be counting the number of mice (prey) and hawk (predator) we find.
The letter “e” will represent the prey (mouse), and the letter “l” will represent the predator (hawk). Count only the squares the teacher has randomly selected. (you could count all of them, but sampling saves you time.)
6. Enter the number of hawks and mice you count in each of the randomly pre-selected square areas onto individual data table.
7. Add up the total number of predator and prey that you counted in the entire field of study. Divide the total number of predator by 25 (to get the squares in the study area). In order to get the estimated total number of predators in the hypothetical forest that year.
8. Repeat step 7 for the prey.
9. Give the teacher your data obtained in steps 7-8. The teacher will prepare the class data table.
10. Use the class data to plot a graph of predators and prey vs. time.
11. Answer the discussion questions.

Sample Discussion Questions


1. In which years was the population of the prey the highest?
2. In which years was the population of the predator the highest?
3. In which years was the population of the prey the lowest?
4. In which years was the population of the predator the lowest?
5. Give three reasons for the population of the prey to increase.
6. Give three reasons for the population of the predator to increase.
7. List three reasons for the population of the prey to decrease.
8. List three reasons for the population of the predator to decrease.
9. The cycle of a simple predator/prey relationship is the number of years between each population peak. What is the cycle for your population?
10. If we were somehow able to study these populations until the year 2010, when should we expect other major increases in the populations?
11. The predator/prey relationship we have modeled in class is a simple relationship because it involves only two animals, the hawk and the mouse. From our vast storehouse of knowledge we know that many animals prey on mice. How might another predator effect our mouse and hawk distribution?
12. This predator/prey graph lacks a lag time between predator population and prey population peaks. Why do the populations lag in a real predator prey graph?

 
Description
The data can be manipulated by the instructor by making "high" population years more or less frequent or even non-cyclical.
This data mimmics the real population data collected in the field (see links below), with the exception of the lag time between predator peaks and prey peaks -a flaw in the system and a teachable moment.

 

 

  
   

References & Links:

A presentation on population studies and sampling

Real data on lynx and snowshoe hare

Population data

Microbiological predator/prey